When I was in elementary school, our class was briefly visited by our school’s headmaster. He was there for a demonstration, probably intended to get us to practice our multiplication tables. “Pick a number”, he said, “And I’ll teach you how to draw a pattern from it.”
The procedure was rather simple:
- Pick a number between 2 and 8 (inclusive).
- Start generating positive multiples of this number. If you picked 8, your multiples would be 8, 16, 24, and so on.
- If a multiple is more than one digit long, sum its digits. For instance, for 16, write 1+6=7. If the digits add up to a number that’s still more than 1 digit long, add up the digits of that number (and so on).
- Start drawing on a grid. For each resulting number, draw that many squares in one direction, and then “turn”. Using 8 as our example, we could draw 8 up, 7 to the right, 6 down, 5 to the left, and so on.
- As soon as you come back to where you started (“And that will always happen”, said my headmaster), you’re done. You should have drawn a pretty pattern!
Sticking with our example of 8, the pattern you’d end up with would be something like this:
Pattern generated by the number 8.
Before we go any further, let’s observe that it’s not too hard to write code to do this.
For instance, the “add digits” algorithm can be naively
written by turning the number into a string (17 becomes "17"), splitting that string into
characters ("17" becomes ["1", "7"]), turning each of these character back into numbers
(the array becomes [1, 7]) and then computing the sum of the array, leaving 8.
|
|
We may now encode the “drawing” logic. At any point, there’s a “direction” we’re going - which
I’ll denote by the Ruby symbols :top, :bottom, :left, and :right. Each step, we take
the current x,y coordinates (our position on the grid), and shift them by n in a particular
direction dir. We also return the new direction alongside the new coordinates.
|
|
The top-level algorithm is captured by the following code, which produces a list of coordinates in the order that you’d visit them.
|
|
I will omit the code for generating SVGs from the body of the article – you can always find the complete source code in this blog’s Git repo (or by clicking the link in the code block above). Let’s run the code on a few other numbers. Here’s one for 4, for instance:
Pattern generated by the number 4.
And one more for 2, which I don’t find as pretty.
Pattern generated by the number 2.
It really does always work out! Young me was amazed, though I would often run out of space on my grid paper to complete the pattern, or miscount the length of my lines partway in. It was only recently that I started thinking about why it works, and I think I figured it out. Let’s take a look!
Is a number divisible by 3?
You might find the whole “add up the digits of a number” thing familiar, and for good reason: it’s one way to check if a number is divisible by 3. The quick summary of this result is,
If the sum of the digits of a number is divisible by 3, then so is the whole number.
For example, the sum of the digits of 72 is 9, which is divisible by 3; 72 itself is correspondingly also divisible by 3, since 24*3=72. On the other hand, the sum of the digits of 82 is 10, which is not divisible by 3; 82 isn’t divisible by 3 either (it’s one more than 81, which is divisible by 3).
Why does this work? Let’s talk remainders.
If a number doesn’t cleanly divide another (we’re sticking to integers here), what’s left behind is the remainder. For instance, dividing 7 by 3 leaves us with a remainder 1. On the other hand, if the remainder is zero, then that means that our dividend is divisible by the divisor (what a mouthful). In mathematics, we typically use to say divides , or, as we have seen above, that the remainder of dividing by is zero.
Working with remainders actually comes up pretty frequently in discrete math. A well-known example I’m aware of is the RSA algorithm, which works with remainders resulting from dividing by a product of two large prime numbers. But what’s a good way to write, in numbers and symbols, the claim that “ divides with remainder ”? Well, we know that dividing yields a quotient (possibly zero) and a remainder (also possibly zero). Let’s call the quotient . [note: It's important to point out that for the equation in question to represent division with quotient and remainder , it must be that is less than . Otherwise, you could write for some , and end up with In plain English, if is bigger than after you've divided, you haven't taken out "as much from your dividend as you could", and the actual quotient is larger than . ]
We only really care about the remainder here, not the quotient, since it’s the remainder that determines if something is divisible or not. From the form of the second equation, we can deduce that is divisible by (it’s literally equal to times , so it must be divisible). Thus, we can write:
There’s another notation for this type of statement, though. To say that the difference between two numbers is divisible by a third number, we write:
Some things that seem like they would work from this “equation-like” notation do, indeed, work. For instance, we can “add two equations” (I’ll omit the proof here; jump down to this section to see how it works):
Multiplying both sides by the same number (call it ) also works (once again, you can find the proof in this section below).
Ok, that’s a lot of notation and other stuff. Let’s talk specifics. Of particular interest is the number 10, since our number system is base ten (the value of a digit is multiplied by 10 for every place it moves to the left). The remainder of 10 when dividing by 3 is 1. Thus, we have:
From this, we can deduce that multiplying by 10, when it comes to remainders from dividing by 3, is the same as multiplying by 1. We can clearly see this by multiplying both sides by . In our notation:
But wait, there’s more. Take any power of ten, be it a hundred, a thousand, or a million. Multiplying by that number is also equivalent to multiplying by 1!
We can put this to good use. Let’s take a large number that’s divisible by 3. This number will be made of multiple digits, like . Note that I do not mean multiplication here, but specifically that each is a number between 0 and 9 in a particular place in the number – it’s a digit. Now, we can write:
We have just found that , or that the sum of the digits is also divisible by 3. The logic we use works in the other direction, too: if the sum of the digits is divisible, then so is the actual number.
There’s only one property of the number 3 we used for this reasoning: that . But it so happens that there’s another number that has this property: 9. This means that to check if a number is divisible by nine, we can also check if the sum of the digits is divisible by 9. Try it on 18, 27, 81, and 198.
Here’s the main takeaway: summing the digits in the way described by my headmaster is
the same as figuring out the remainder of the number from dividing by 9. Well, almost.
The difference is the case of 9 itself: the remainder here is 0, but we actually use 9
to draw our line. We can actually try just using 0. Here’s the updated sum_digits code:
def sum_digits(n)
n % 9
end
The results are similarly cool:
Pattern generated by the number 8. Pattern generated by the number 4. Pattern generated by the number 2.
Sequences of Remainders
So now we know what the digit-summing algorithm is really doing. But that algorithm isn’t all there is to it! We’re repeatedly applying this algorithm over and over to multiples of another number. How does this work, and why does it always loop around? Why don’t we ever spiral farther and farther from the center?
First, let’s take a closer look at our sequence of multiples. Suppose we’re working with multiples of some number . Let’s write for the th multiple. Then, we end up with:
This is actually called an arithmetic sequence; for each multiple, the number increases by .
Here’s a first seemingly trivial point: at some time, the remainder of will repeat. There are only so many remainders when dividing by nine: specifically, the only possible remainders are the numbers 0 through 8. We can invoke the pigeonhole principle and say that after 9 multiples, we will have to have looped. Another way of seeing this is as follows:
The 10th multiple is equivalent to n, and will thus have the same remainder. The looping may happen earlier: the simplest case is if we pick 9 as our , in which case the remainder will always be 0.
Repeating remainders alone do not guarantee that we will return to the center. The repeating sequence 1,2,3,4 will certainly cause a spiral. The reason is that, if we start facing “up”, we will always move up 1 and down 3 after four steps, leaving us 2 steps below where we started. Next, the cycle will repeat, and since turning four times leaves us facing “up” again, we’ll end up getting further away. Here’s a picture that captures this behvior:
Spiral generated by the number 1 with divisor 4.
And here’s one more where the cycle repeats after 8 steps instead of 4. You can see that it also leads to a spiral:
Spiral generated by the number 1 with divisor 8.
From this, we can devise a simple condition to prevent spiraling – the length of the sequence before it repeats cannot be a multiple of 4. This way, whenever the cycle restarts, it will do so in a different direction: backwards, turned once to the left, or turned once to the right. Clearly repeating the sequence backwards is guaranteed to take us back to the start. The same is true for the left and right-turn sequences, though it’s less obvious. If drawing our sequence once left us turned to the right, drawing our sequence twice will leave us turned more to the right. On a grid, two right turns are the same as turning around. The third repetition will then undo the effects of the first one (since we’re facing backwards now), and the fourth will undo the effects of the second.
There is an exception to this multiple-of-4 rule: if a sequence makes it back to the origin right before it starts over. In that case, even if it’s facing the very same direction it started with, all is well – things are just like when it first started, and the cycle repeats. I haven’t found a sequence that does this, so for our purposes, we’ll stick with avoiding multiples of 4.
Okay, so we want to avoid cycles with lengths divisible by four. What does it mean for a cycle to be of length k? It effectively means the following:
If we could divide both sides by , we could go one more step:
That is, would be divisible by 9! This would contradict our choice of to be between 2 and 8. What went wrong? Turns out, it’s that last step: we can’t always divide by . Some values of are special, and it’s only those values that can serve as cycle lengths without causing a contradiction. So, what are they?
They’re values that have a common factor with 9 (an incomplete explanation is in this section below). There are many numbers that have a common factor with 9; 3, 6, 9, 12, and so on. However, those can’t all serve as cycle lengths: as we said, cycles can’t get longer than 9. This leaves us with 3, 6, and 9 as possible cycle lengths, none of which are divisible by 4. We’ve eliminated the possibility of spirals!
Generalizing to Arbitrary Divisors
The trick was easily executable on paper because there’s an easy way to compute the remainder of a number when dividing by 9 (adding up the digits). However, we have a computer, and we don’t need to fall back on such cool-but-complicated techniques. To replicate our original behavior, we can just write:
def sum_digits(n)
x = n % 9
x == 0 ? 9 : x
end
But now, we can change the 9 to something else. There are some numbers we’d like to avoid - specifically,
we want to avoid those numbers that would allow for cycles of length 4 (or of a length divisible by 4).
If we didn’t avoid them, we might run into infinite loops, where our pencil might end up moving
further and further from the center.
Actually, let’s revisit that. When we were playing with paths of length while dividing by 9, we noted that the only possible values of are those that share a common factor with 9, specifically 3, 6 and 9. But that’s not quite as strong as it could be: try as you might, but you will not find a cycle of length 6 when dividing by 9. The same is true if we pick 6 instead of 9, and try to find a cycle of length 4. Even though 4 does have a common factor with 6, and thus is not ruled out as a valid cycle by our previous condition, we don’t find any cycles of length 4.
So what is it that really determines if there can be cycles or not?
Let’s do some more playing around. What are the actual cycle lengths when we divide by 9? For all but two numbers, the cycle lengths are 9. The two special numbers are 6 and 3, and they end up with a cycle length of 3. From this, we can say that the cycle length seems to depend on whether or not our has any common factors with the divisor.
Let’s explore this some more with a different divisor, say 12. We fill find that 8 has a cycle length of 3, 7 has a cycle length of 12, 9 has a cycle length of 4. What’s happening here? To see, let’s divide 12 by these cycle lengths. For 8, we get (12/3) = 4. For 7, this works out to 1. For 9, it works out to 3. These new numbers, 4, 1, and 3, are actually the greatest common factors of 8, 7, and 3 with 12, respectively. The greatest common factor of two numbers is the largest number that divides them both. We thus write down our guess for the length of a cycle:
Where is our divisor, which has been 9 until just recently, and is the greatest common factor of and . This equation is in agreement with our experiment for , too. Why might this be? Recall that sequences with period imply the following congruence:
Here I’ve replaced 9 with , since we’re trying to make it work for any divisor, not just 9. Now, suppose the greatest common divisor of and is some number . Then, since this number divides and , we can write for some , and for some . We can rewrite our congruence as follows:
We can simplify this a little bit. Recall that what this congruence really means is that the difference of and , which is just , is divisible by :
But if divides , it must be that divides ! This, in turn, means we can write:
Can we distill this statement even further? It turns out that we can. Remember that we got and by dividing and by their greatest common factor, . This, in turn, means that and have no more common factors that aren’t equal to 1 (see this section below). From this, in turn, we can deduce that is not relevant to dividing , and we get:
That is, we get that must be divisible by . Recall that we got by dividing by , which is our largest common factor – aka . We can thus write:
Let’s stop and appreciate this result. We have found a condition that is required for a sequnce of remainders from dividing by (which was 9 in the original problem) to repeat after numbers. Furthermore, all of our steps can be performed in reverse, which means that if a matches this conditon, we can work backwards and determine that a sequence of numbers has to repeat after steps.
Multiple s will match this condition, and that’s not surprising. If a sequence repeats after 5 steps, it also repeats after 10, 15, and so on. We’re interested in the first time our sequences repeat after taking any steps, which means we have to pick the smallest possible non-zero value of . The smallest number divisible by is itself. We thus confirm our hypothesis:
Lastly, recall that our patterns would spiral away from the center whenever a is a multiple of 4. Now that we know what
is, we can restate this as “ is divisible by 4”. But if we pick
, the greatest common factor has to be (see this section below), so we can even further simplify this “ is divisible by 4”.
Thus, we can state simply that any divisor divisible by 4 is off-limits, as it will induce loops.
For example, pick . Running our algorithm
[note:
Did you catch that? From our work above, we didn't just find a condition that would prevent spirals;
we also found the precise number that would result in a spiral if this condition were violated!
This is because our proof is constructive: instead of just claiming the existence
of a thing, it also shows how to get that thing. Our proof in the earlier section (which
claimed that the divisor 9 would never create spirals) went by contradiction, which was
not constructive. Repeating that proof for a general wouldn't have told us
the specific numbers that would spiral.
This is the reason that direct proofs tend to be preferred over proofs by contradiction.
]
we indeed find an infinite
spiral:
Spiral generated by the number 3 with divisor 4.
Let’s try again. Pick ; then, for , we also get a spiral:
Spiral generated by the number 7 with divisor 8.
A poem comes to mind:
Turning and turning in the widening gyre
The falcon cannot hear the falconner;
Fortunately, there are plenty of numbers that are not divisible by four, and we can pick any of them! I’ll pick primes for good measure. Here are a few good ones from using 13 (which corresponds to summing digits of base-14 numbers):
Pattern generated by the number 8 in base 14. Pattern generated by the number 4 in base 14.
Here’s one from dividing by 17 (base-18 numbers).
Pattern generated by the number 5 in base 18.
Finally, base-30:
Pattern generated by the number 2 in base 30.
Pattern generated by the number 6 in base 30.
Generalizing to Arbitrary Numbers of Directions
What if we didn’t turn 90 degrees each time? What, if, instead, we turned 120 degrees (so that turning 3 times, not 4, would leave you facing the same direction you started)? We can pretty easily do that, too. Let’s call this number of turns . Up until now, we had .
First, let’s update our condition. Before, we had “ cannot be divisible by 4”. Now, we aren’t constraining ourselves to only 4, but rather using a generic variable . We then end up with “ cannot be divisible by ”. For instance, suppose we kept our divisor as 9 for the time being, but started turning 3 times instead of 4. This violates our divisibility condtion, and we once again end up with a spiral:
Pattern generated by the number 8 in base 10 while turning 3 times.
If, on the other hand, we pick and , we get patterns for all numbers just like we hoped. Here’s one such pattern:
Pattern generated by the number 7 in base 9 while turning 3 times.
Hold on a moment; it’s actully not so obvious why our condition still works. When we just turned on a grid, things were simple. As long as we didn’t end up facing the same way we started, we will eventually perform the exact same motions in reverse. The same is not true when turning 120 degrees, like we suggested. Here’s an animated circle all of the turns we would make:

Orientations when turning 120 degrees
We never quite do the exact opposite of any one of our movements. So then, will we come back to the origin anyway? Well, let’s start simple. Suppose we always turn by exactly one 120-degree increment (we might end up turning more or less, just like we may end up turning left, right, or back in the 90 degree case). Each time you face a particular direciton, after performing a cycle, you will have moved some distance away from when you started, and turned 120 degrees. If you then repeat the cycle, you will once again move by the same offset as before, but this time the offset will be rotated 120 degrees, and you will have rotated a total of 240 degrees. Finally, performing the cycle a third time, you’ll have moved by the same offset (rotated 240 degrees).
If you overaly each offset such that their starting points overlap, they will look very similar to that circle above. And now, here’s the beauty: you can arrange these rotated offsets into a triangle:
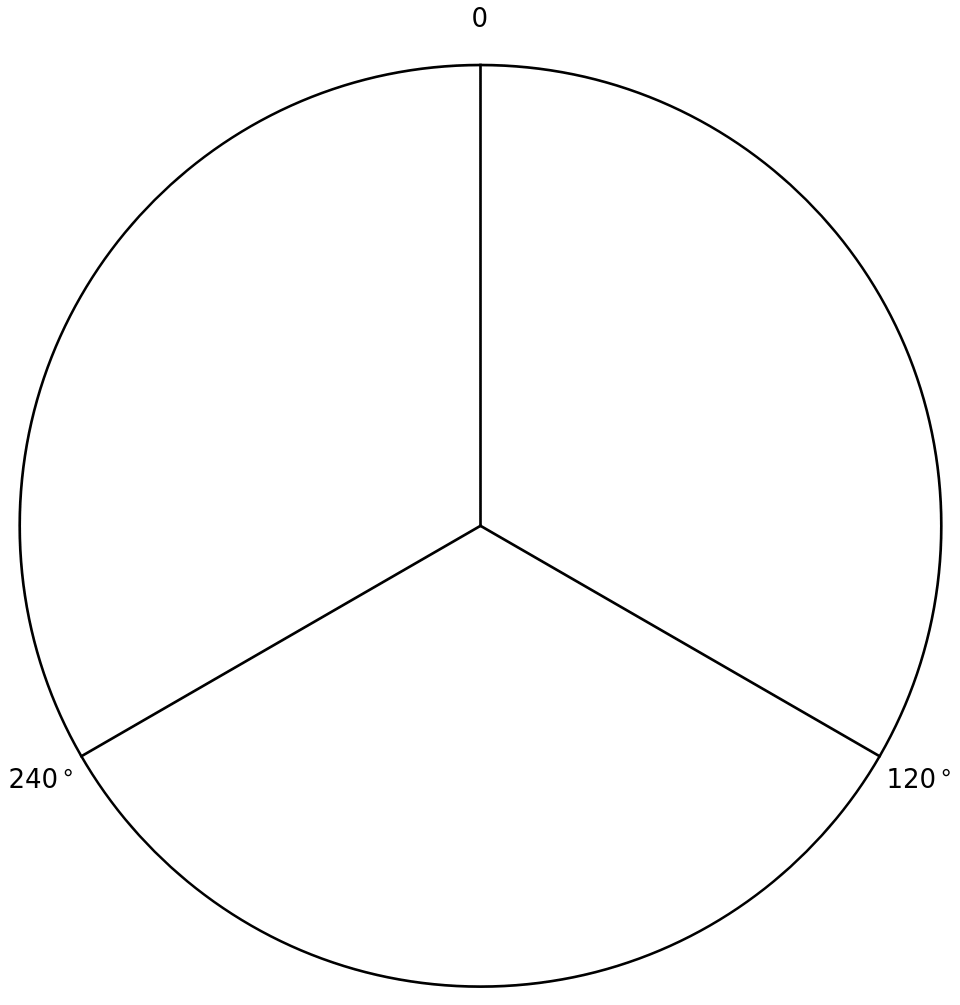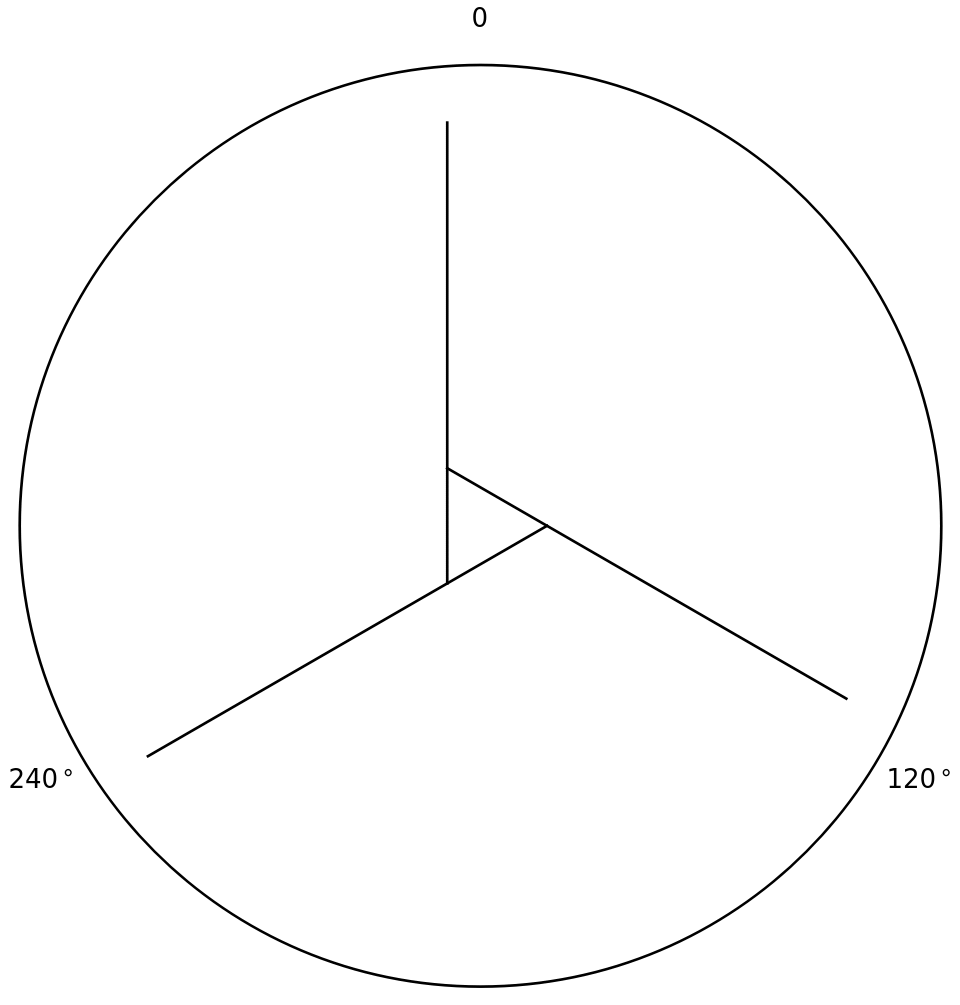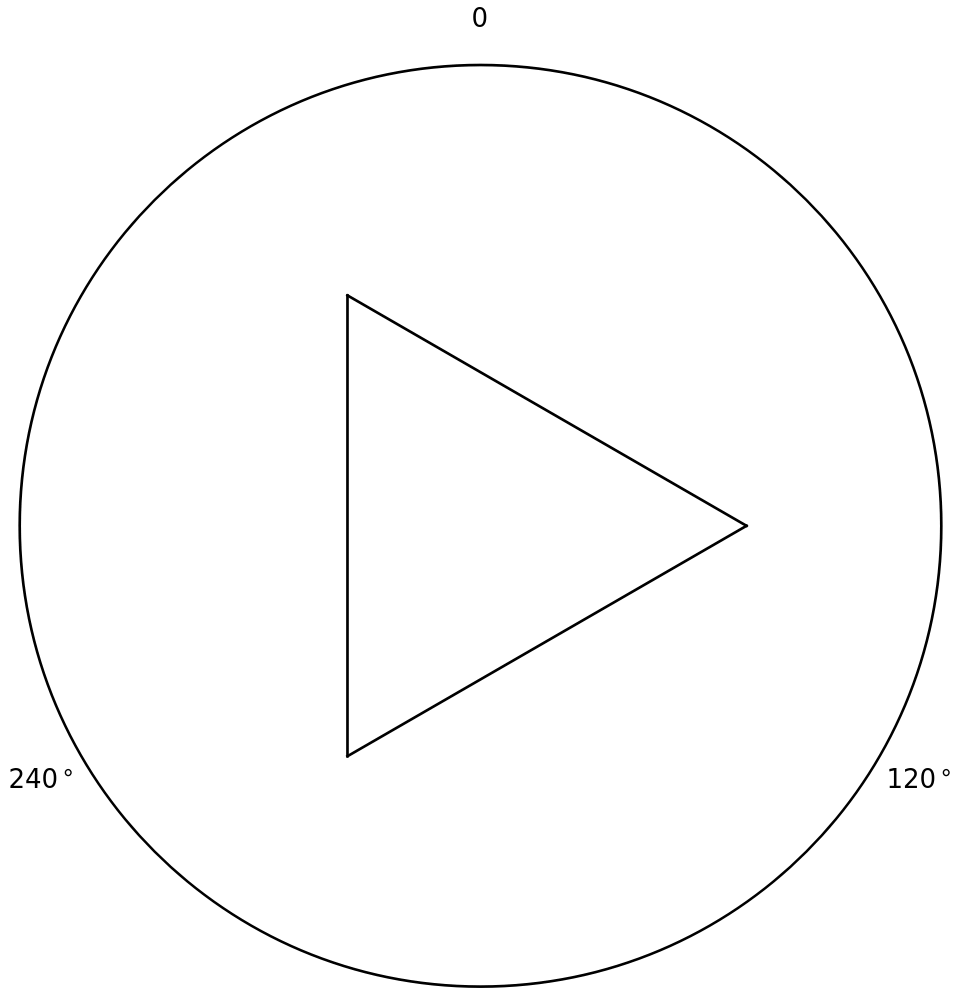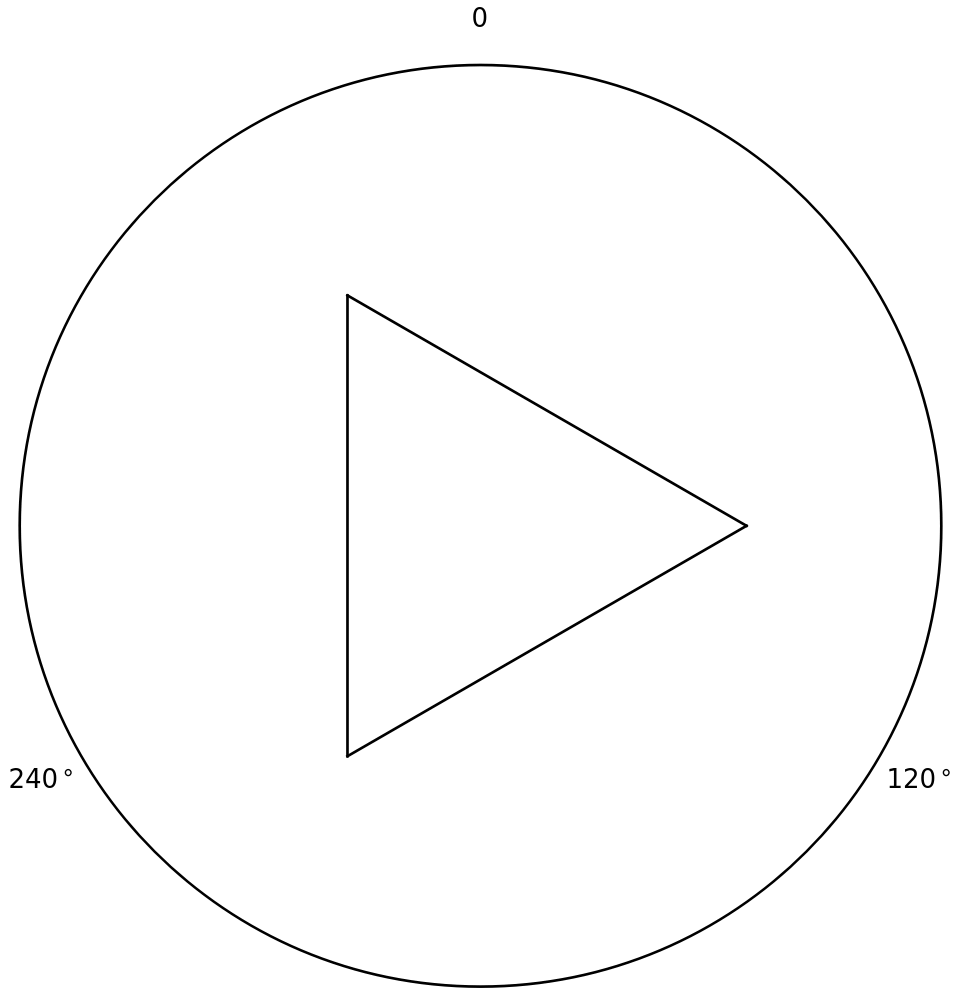
Triangle formed by three 120-degree turns.
As long as you rotate by the same amount each time (and you will, since the cycle length determines how many times you turn, and the cycle length never changes), you can do so for any number of directions. For instance, here’s a similar visualization in which there are 5 possible directions, and where each turn is consequently 72 degrees:
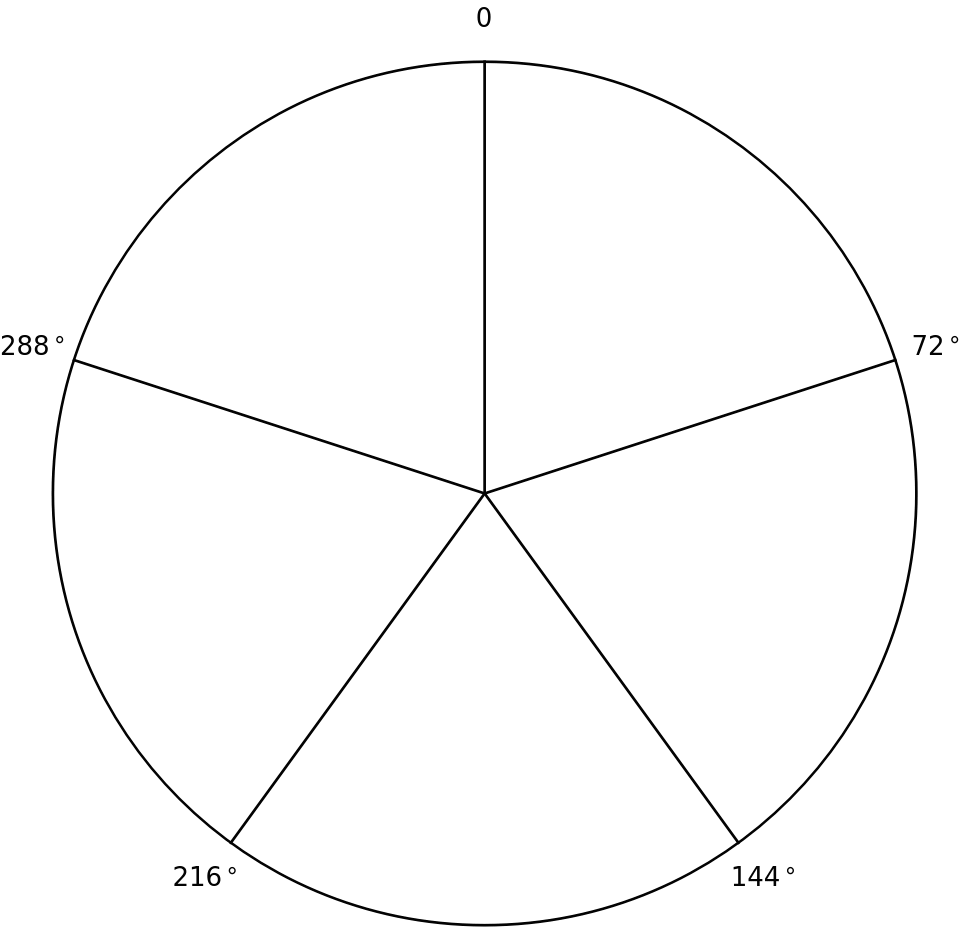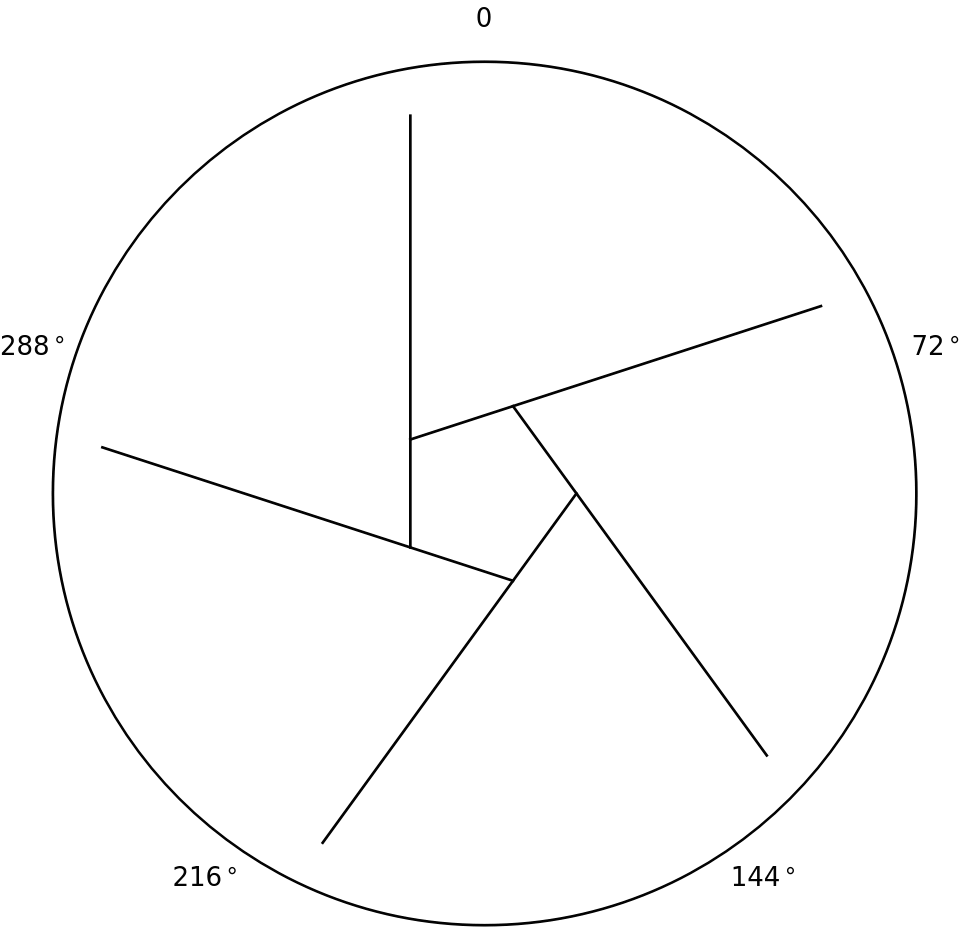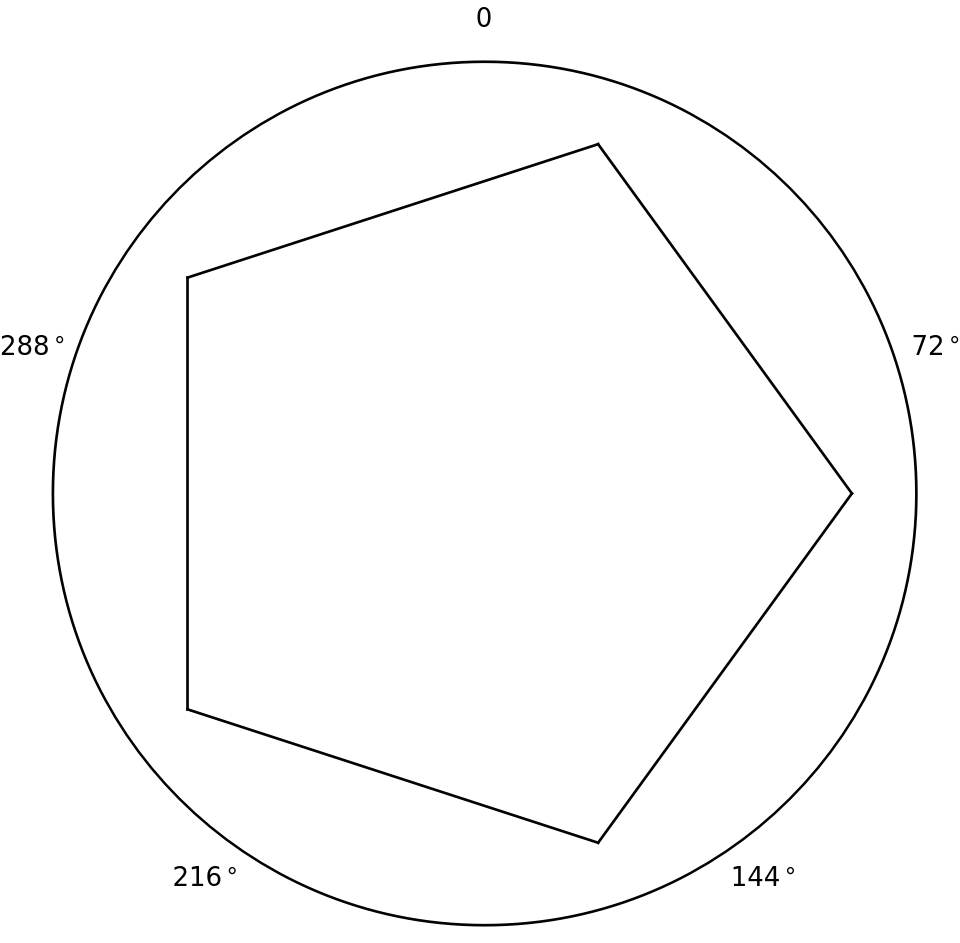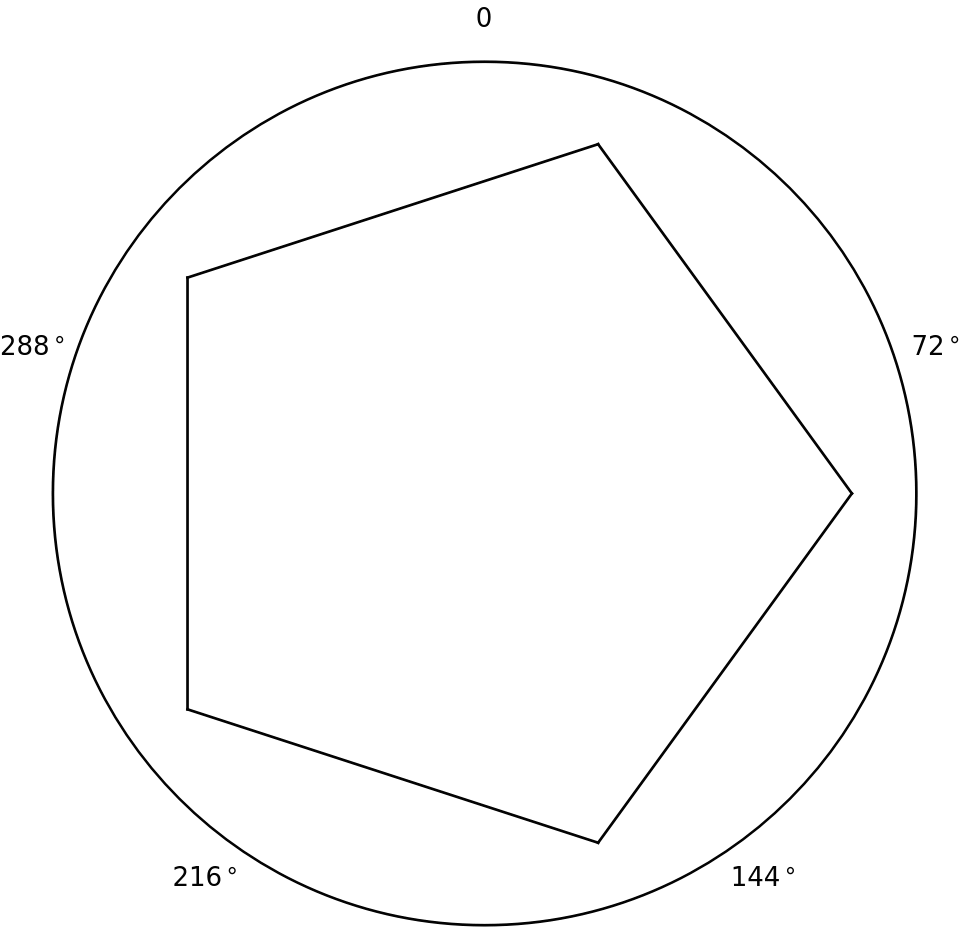
Pentagon formed by five 72-degree turns.
Each of these polygon shapes forms a loop. If you walk along its sides, you will eventually end up exactly where you started. This confirms that if you end up making one turn at the end of each cycle, you will eventually end up right where you started.
Things aren’t always as simple as making a single turn, though. Let’s go back to the version of the problem in which we have 3 possible directions, and think about what would happen if we turned by 240 degrees at a time: 2 turns instead of 1?
Even though we first turn a whole 240 degrees, the second time we turn we “overshoot” our initial bearing, and end up at 120 degrees compared to it. As soon as we turn 240 more degrees (turning the third time), we end up back at 0. In short, even though we “visited” each bearing in a different order, we visited them all, and exactly once at that. Here’s a visualization:

Orientations when turning 120 degrees, twice at a time
Note that even though in the above picture it looks like we’re just turning left instead of right, that’s not the case; a single turn of 240 degrees is more than half the circle, so our second bearing ends up on the left side of the circle even though we turn right.
Just to make sure we really see what’s happening, let’s try this when there are 5 possible directions, and when we still make two turns (now of 72 degrees each)

Orientations when turning 72 degrees, twice at a time
Let’s try put some mathematical backing to this “visited them all” idea, and turning in general. First, observe that as soon as we turn 360 degrees, it’s as good as not turning at all - we end up facing up again. If we turned 480 degrees (that is, two turns of 240 degrees each), the first 360 can be safely ignored, since it puts us where we started; only the 120 degrees that remain are needed to figure out our final bearing. In short, the final direction we’re facing is the remainder from dividing by 360. We already know how to formulate this using modular arithmetic: if we turn degrees times, and end up at final bearing (remainder) , this is captured by:
Of course, if we end up facing the same way we started, we get the familiar equivalence:
Even though the variables in this equivalence mean different things now than they did last time we saw it, the mathematical properties remain the same. For instance, we can say that after turns, we’ll end up facing the way that we started.
So far, so good. What I don’t like about this, though, is that we have all of these numbers of degrees all over our equations: 72 degrees, 144 degrees, and so forth. However, something like 73 degrees (if there are five possible directions) is just not a valid bearing, and nor is 71. We have so many possible degrees (360 of them, to be exact), but we’re only using a handful! That’s wasteful. Instead, observe that for possible turns, the smallest possible turn angle is . Let’s call this angle (theta). Now, notice that we always turn in multiples of : a single turn moves us degrees, two turns move us degrees, and so on. If we define to be the number of turns that we find ourselves rotated by after a single cycle, we have , and our turning equation can be written as:
Now, once again, recall that the above equivalence is just notation for the following:
And finally, observing that , we have:
This equivalence says the same thing as our earlier one; however, instead of being in terms of degrees, it’s in terms of the number of turns and the turns-per-cycle . Now, recall once again that the smallest number of steps for which this equivalence holds is .
We’re close now: we have a sequence of steps that will lead us back to the beginning. What’s left is to show that these steps are evenly distributed throughout our circle, which is the key property that makes it possible for us to make a polygon out of them (and thus end up back where we started).
To show this, say that we have a largest common divisor , and that and . We can once again “divide through” by , and get:
Now, we know that (see this section below), and thus:
That is, our cycle will repeat after remainders. But wait, we’ve only got possible remainders: the numbers through ! Thus, for a cycle to repeat after remainders, all possible remainders must occur. For a concrete example, take ; our remainders will be the set . Now, let’s “multiply back through” by :
We still have possible remainders, but this time they are multiplied by . For example, taking to once again be equal to , we have the set of possible remainders . The important bit is that these remainders are all evenly spaced, and that space between them is .
Let’s recap: we have confirmed that for possible turns (4 in our original formulation), and turns at a time, we will always loop after steps, evenly spaced out at turns. No specific properties from or are needed for this to work. Finally, recall from the previous section that is zero (and thus, our pattern breaks down) whenever the divisor (9 in our original formulation) is itself divisible by . And so, as long as we pick a system with possible directions and divisor , we will always loop back and create a pattern as long as ( does not divide ).
Let’s try it out! There’s a few pictures below. When reading the captions, keep in mind that the base is one more than the divisor (we started with numbers in the usual base 10, but divided by 9).
Pattern generated by the number 1 in base 8 while turning 5 times.
Pattern generated by the number 3 in base 5 while turning 7 times.
Pattern generated by the number 3 in base 12 while turning 6 times.
Pattern generated by the number 2 in base 12 while turning 7 times.
Conclusion
Today we peeked under the hood of a neat mathematical trick that was shown to me by my headmaster over 10 years ago now. Studying what it was that made this trick work led us to play with the underlying mathematics some more, and extend the trick to more situations (and prettier patterns). I hope you found this as interesting as I did!
By the way, the kind of math that we did in this article is most closely categorized as number theory. Check it out if you’re interested!
Finally, a huge thank you to Arthur for checking my math, helping me with proofs, and proofreading the article.
All that remains are some proofs I omitted from the original article since they were taking up a lot of space (and were interrupting the flow of the explanation). They are listed below.
Referenced Proofs
Adding Two Congruences
Claim: If for some numbers , , , , and , we have and , then it’s also true that .
Proof: By definition, we have and . This, in turn, means that for some and , and . Add both sides to get:
Multiplying Both Sides of a Congruence
Claim: If for some numbers , , and , we have then we also have that .
Proof: By definition, we have . Since multiplying but cannot make it not divisible by , we also have . Distributing , we have . By definition, this means .
Invertible Numbers Share no Factors with
Claim: A number is only invertible (can be divided by) in if and share no common factors (except 1).
Proof: Write for the greatest common factor divisor of and . Another important fact (not proven here, but see something like this), is that if , then the smallest possible number that can be made by adding and subtracting s and s is . That is, for some and , the smallest possible positive value of is .
Now, note that . Multiplying both sides by , get . This, in turn, means that the smallest possible value of is . If is bigger than 1 (i.e., if and have common factors), then we can’t pick such that , since we know that is the least possible value we can make. There is therefore no multiplicative inverse to . Alternatively worded, we cannot divide by .
Numbers Divided by Their Have No Common Factors
Claim: For any two numbers and and their largest common factor , if and , then and have no common factors other than 1 (i.e., ).
Proof: Suppose that and do have sommon factor, . In that case, we have and for some and . Then, we have , and . From this, it’s clear that both and are divisible by . Since is greater than , is greater than . But our assumptions state that is the greatest common divisor of and ! We have arrived at a contradiction.
Thus, and cannot have a common factor other than 1.
Divisors of and .
Claim: For any , . That is, and share no common divisors.
Proof: Suppose some number divides both and . In that case, we can write , and for some and . Subtracting one equation from the other:
But this means that 1 is divisible by ! That’s only possible if . Thus, the only number that divides and is 1; that’s our greatest common factor.