Disclaimer: though “my compiler code” makes for a fun title, I do not claim exclusive credit for any of the C++ code in the Chapel compiler that I mention in this post. The code is “mine” in the sense that I was debugging changes I was making, and perhaps also in the sense that I was working with it.
I work as a compiler developer on the Chapel team. Recently, while thinking through a change to some code, I caught myself making wishes: “if only I could have a computer check this property for me”. Having at some point seen Hillel Wayne’s post about the release of Alloy 6, I thought I’d give it a go. In this post, I describe my experience applying Alloy to a real part of the Chapel compiler. I’d never touched Alloy before this, so be warned: this is what I came up with on my own attempt, and I may well be doing something fairly silly by the standards of “real” Alloy users.
The Problem at Hand
One of the things that a language like Chapel has to do is called resolution,
which is the process of figuring out what each identifier, like x, refers to,
and what its type is. Even the first part of that is pretty complicated, what
with public and private variables, methods (which can be declared outside
of their receiver type in Chapel), and more…
Scope resolution in Chapel is further complicated by the fact that the same scope might need to be searched multiple times, in different contexts. Let me start with a few examples to illustrate what I mean. Here’s the first program:
|
|
If you don’t know Chapel (and you probably don’t!) this program already merits a fair bit of explanation. I’ve collapsed it for the sake of visual clarity; feel free to expand the below section to learn more about the language features used in the program above.
Click here for an explanation of the above code snippet
A module in Chapel (declared via a module keyword)
is just a collection of definitions. Such definitions could include variables,
methods, classes and more. Putting them in a module helps group them.
A class in Chapel (declared via a class keyword) is much like a class in
object oriented languages. The class C that we’re creating on line 2 doesn’t
have any fields or methods – at least not yet. We will, however, add methods
to it using Chapel’s secondary method mechanism (more on that in a moment).
The proc keyword is used to create functions and methods. On line 5, we
create a procedure called foo that does nothing. On line 8, because we
write C.foo instead of just foo, we’re actually creating a method on
the class C we declared earlier. This method does nothing too. Notice
that although declaring classes in Chapel works about the same as declaring
classes in other languages, it’s fairly unusual to be able to declare a
class method (like the foo on line 8 in this case) outside of the class C { ... } section of code. This is part of the reason that Chapel method
resolution is complicated (methods can be declared anywhere!). The only
other language that I know of that supports this feature is Kotlin with its
extension function
mechanism, but it’s possible
that other languages have similar functionality.
The interesting part of the snippet is the body of the doSomething method.
It has a call to foo: but which foo is it referring to? There are two:
the regular procedure (non-method) foo, declared on line 5, and the
method C.foo declared on line 8. In Chapel, the rules dictate that when
such a situation arises, and a fitting method is found, the method is
preferred to the non-method. In the rewritten version of the Chapel compiler,
titled Dyno, this disambiguation is achieved by first searching the scopes
visible from the class C for methods only. In this particular example,
the two scopes searched will be:
- The inside of class
C. The class itself doesn’t define any methods, so nothing is found. - The module in which
Cis defined (Min this case). This module does have a method, the one on line 8, so that one is returned.
Only if methods are not found are non-methods considered. In this situation, the search order will be as follows:
- The inside of
C.doSomethingwill be searched.doSomethingdoesn’t declare anything, so the search will come up empty. - The module in which
C.doSomethingis defined (Magain) will be searched. This time, both methods and non-methods will be considered. Since we’re considering a hypothetical situation in which the methodC.fooisn’t there (otherwise it would’ve been found earlier), the only thing that will be found will be the non-methodfoo.
Notice that we’ve already had to search the module M twice, looking for
different things each time. First, we were looking for only methods, but
later, we were looking for anything. However, this isn’t as complicated as
things can get. The simplifying aspect of this program is that both doSomething
and C are defined inside the module M, and therefore have access to its
private methods and procedures. If we extracted C.doSomething into its
own separate module, the program would look like this.
|
|
Since doSomething is now in another module, it can’t just access the foos from
M1 willy-nilly. There are a few ways to get the things that were declared in another module out
and make use of them. I opted for a use statement, which, in its simplest form,
just brings all the declarations inside the used module into the current scope. Thus,
the use statement on line 11 would bring all things declared in M1 into
the scope inside M2. There’s a catch, though. Since M2 is not declared
inside M1, a use statement will not be able to bring in private symbols
from M1 (they’re private for a reason!). So, this time, when searching the scope
for M1, we will have to search only for public symbols. That’s another,
different way of searching M1. So far, we’ve seen three:
- Search
M1for any symbol. - Search
M1for methods only. - Search
M1for public symbols only.
Dyno introduces more ways to search within a scope, including combinations of search types, such as looking only for public methods. To represent the various search configurations, the Dyno team came up with using a bitfield of flags, each of which indicated a necessary condition for a symbol to be returned. A bitfield with flags set for two properties (like “public” and “method”) requires that both such properties be found on each symbol that’s returned from a scope. This led to C++ code along the lines of:
auto allPublicSymbols = Flags::PUBLIC;
auto allPublicMethods = Flags::PUBLIC | Flags::METHOD;
It also turned out convenient to add negative versions of each flag
(NOT_PUBLIC for private symbols, NOT_METHOD for regular old procedures
and other definitions, and so on. So, some other possible flag combinations
include:
auto allNonMethods = Flags::NOT_METHOD;
auto privateMethods = Flags::NOT_PUBLIC | Flags::METHOD;
Given these flags, there are some situations in which checking a scope a second time is redundant, in that it is guaranteed to find no additional symbols. For instance, if you search a scope for all public symbols, and then subsequently search for all public methods, you will only find duplicates – after all, all public methods are public symbols. Most generally, this occurs when a second search has all the flags from a previous search, and maybe more. In math lingo, if the set of flags checked the first time is a subset of the set of flags checked the second time, it’s guaranteed not to find anything new.
In Dyno, we like to avoid additional work when we can. To do so, we track which scopes have already been searched, and avoid searching them again. Since what comes up from a search depends on the flags, we store the flags alongside the scopes we’ve checked. If we find that the previously-checked bitfield is a subset of the current bitset, we just skip the search.
But then, what if it isn’t a subset? Another concern here is avoiding duplicate results (it’s easier to check for duplicate definitions if you know a symbol is only returned from a search once). So, another feature of Dyno’s scope search is an additional bitfield of what to exclude, which we set to be the previous search’s filter. So if the first search looked for symbols matching description , and the second search is supposed to look for symbols matching description , then really we do a search for (that is, and not ).
One last thing: what happens if there were two previous searches? What we need is to to somehow combine the two filters into one. Taking a cue from a previous example, in which “public” was followed by “public methods”, we can observe that since the second search has additional flags, it’s more restrictive, and thus guaranteed to not find anything. So we try to create the least restrictive bitfield possible, by taking an intersection of the flags used.
Actually, that last point is not quite correct in every possible case (taking the intersection is not always the right thing to do). However, running the code through our test suite, we did not notice any cases in which it misbehaved. So, noting the potential issue in a comment, we moved on to other things.
That is, until I decided that it was time to add another possible flag to the bitfield. At that point, sitting and trying to reason about the possible cases, I realized that it would be much nicer to describe this mathematically, and have a model checker generate outlandish scenarios for me.
Modeling Flags and Bitsets in Alloy
Flags are represented on the C++ side as an enum (with custom indexing so
as to make each flag be exactly one bit). I checked, and it looked like
Alloy had an enum feature, too! I started off by making an enum of the
flags I wanted to play with.
|
|
We haven’t seen the MethodOrField flag, but it’s an important one. It
turns out that it’s much more common to look for anything that could be
part of a class, rather than just its methods. This flag is itself an “or”
of two properties (something being a method and something being a class
field). Note that this is not the same as having two flags, Method and
Field, and always including them together (because that would be an
“and”, not an “or”).
Notice also that the list of flags doesn’t include the negative versions.
Since the negative versions are one-for-one with the positive ones, I
instead chose to represent bitfields as simply two sets: one set of
“positive” flags, in which the presence of e.g. Method indicates that the
METHOD flag was set, and one set of “negative” flags, in which the
presence of Method indicates that NOT_METHOD was set. This way, I’m
guaranteed that there’s a positive and negative version of each flag,
automatically. Here’s how I wrote that in Alloy.
|
|
This definition (a signature in Alloy terms) specifies what a bitfield is
like, but not any operations on it. My next order of business is to define
some common functionality on bitfields. Alloy is all about
relations and
predicates,
so for all of these, I had to effectively write something that checks if
some condition holds for some arguments. This might seem abstract; as an
example, here’s bitfieldEmpty, which checks that a bitfield has no flags
set.
|
|
The # operator in Alloy is used to check the size of a set. So, to check
if a bitfield is empty, I simply check if there are neither positive nor
negative flags. Probably the most unusual aspect of this piece of code is
that equality is written as =, as opposed to == like in most common
languages. This is because, like I said, Alloy is all about relations and
predicates, and not at all about imperative manipulation of data. So,
there’s no need to reserve = for assignment.
The next step from here is a predicate that accepts two arguments,
bitfieldEqual. As its name suggests, this predicate accepts two
bitfields, and makes sure they have exactly the same flags set.
|
|
So far, this has been pretty similar to just writing boolean functions in a
language like C++. However, the similarity is only superficial. An easy way
to see that is to try to determine the intersection of two bitfields –
that’s the operation we will be having to model, since the Dyno
implementation uses & to combine filter sets. In a language like C++, you
might write a function like the following, in which you accept two bitfield
arguments and return a new bitfield.
Bitfield intersection(Bitfield b1, Bitfield b2) { /* ... */ }
However, in Alloy, you can’t create a new bitfield, nor return something
from a pred that isn’t a boolean. Instead, you describe how the inputs
will be related to the output. So, to model a binary function, you end up
with a three-parameter predicate: two inputs, and one output. But how
does the output of a bitfield intersection connect to the two operands
being intersected? Well, its two flag sets will be intersections of the
flag sets of the inputs!
|
|
Next, let’s talk about what flags do. They are used to include and
exclude symbols based on certain properties. One property is being a
method: a METHOD flag requires this property, whereas a NOT_METHOD flag
ensures that a symbol does not have it. Another property is being a public
definition: if a symbol isn’t public, it’ll be ignored by searches with the
PUBLIC flag set. Just like a bitfield can have multiple flags, a symbol
can have multiple properties (e.g., a public method). Unlike our bitfields,
though, we won’t be modeling symbols as having both positive and negative
properties. That is to say, we won’t have a “not public” property: the
absence of the “public” property will be enough to make something private.
Here’s the Alloy definition for everything I just said:
|
|
Now, we can specify how flags in a bitfield relate to properties on a
symbol. We can do so by saying which flags match which properties. The
Method flag, for instance, will be satisfied by the PMethod property.
The MethodOrField flag is more lenient, and will be satisfied by either
PMethod or PField. Here’s a predicate flagMatchesProperty that
encodes all the flag-property combinations:
|
|
A bitfield matching a symbol is a little bit more complicated. Said informally, the condition for a bitfield matching a symbol is twofold:
- Every single positive flag, like
METHOD, must be satisfied by a property on the symbol. - None of the negative flags, like
NOT_METHOD, must be satisfied by a property on the symbol (that is to say, ifMethodis in the negative flags set, then the symbol must not havePMethodproperty). It is more conveniently to formulate this – equivalently – as follows: for each negative flag, there must not be a property that satisfies it.
Each of the above two conditions translates quite literally into Alloy:
|
|
We can read line 73 as “for each flag in a bitfield’s positive flags, there must be some property in the symbol that matches it”. Similarly, line 74 can be read out loud as “for each flag in the negative flags, no property in the symbol must match it”.
We’ve written a fair bit of Alloy. If you’re anything like me, you might be getting a bit twitchy: how do we even check that any of this works? For this, we’ll need to run our model. We will give Alloy a claim, and ask it to find a situation in which that claim holds true. The simplest claim is “there exists a bitfield”.
|
|
Executing this model yields a pretty interesting bitfield: one in which every single flag is set – both the positive and negative versions.
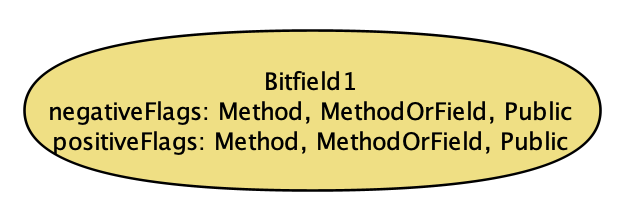
Alloy’s output satisfying “a bit field exists”
That’s a little bit ridiculous: this bitfield will never match anything! You can’t be and not be a method at the same time, for instance. For for a more interesting example, let’s ask for a bitfield that matches some symbol.
|
|
The output here is pretty interesting too. Alloy finds a symbol and a bitfield that matches it, but they’re both empty. In effect, it said: “if you don’t specify any filters, any private definition will match”. Fair enough, of course, but a curious departure from the previous maximalist “put in all the flags!” approach.
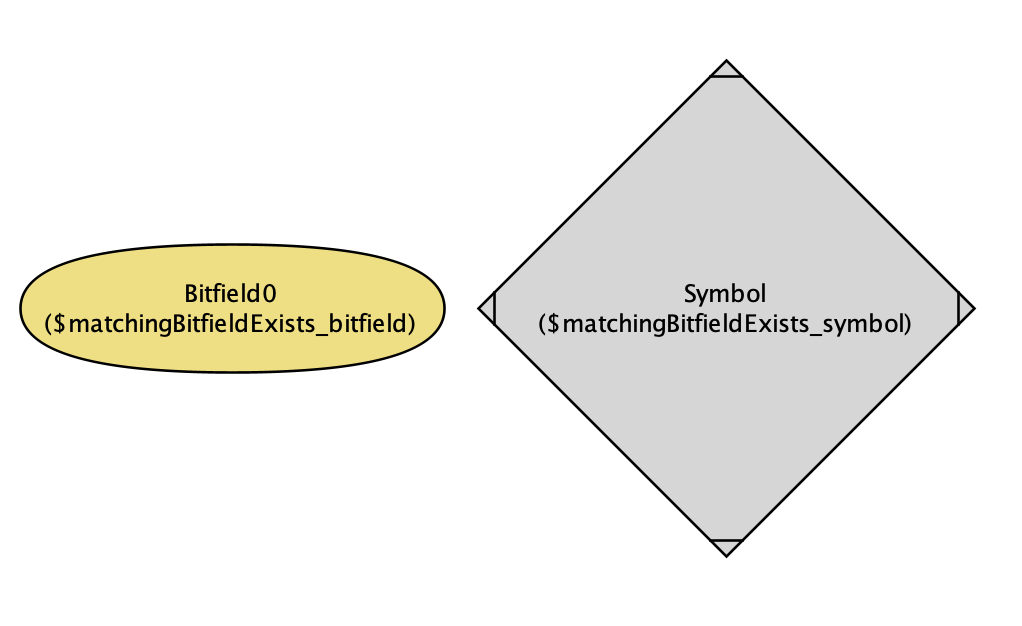
Alloy’s output satisfying “a bit field that matches a symbol exists”
Let’s try nudge it towards a more interesting case. I’m going to ask for a filter with one positive and one negative flag, and a symbol with two properties.
|
|
The results are more interesting this time: we get a filter for private methods, and a private symbol that was… both a field and a method?
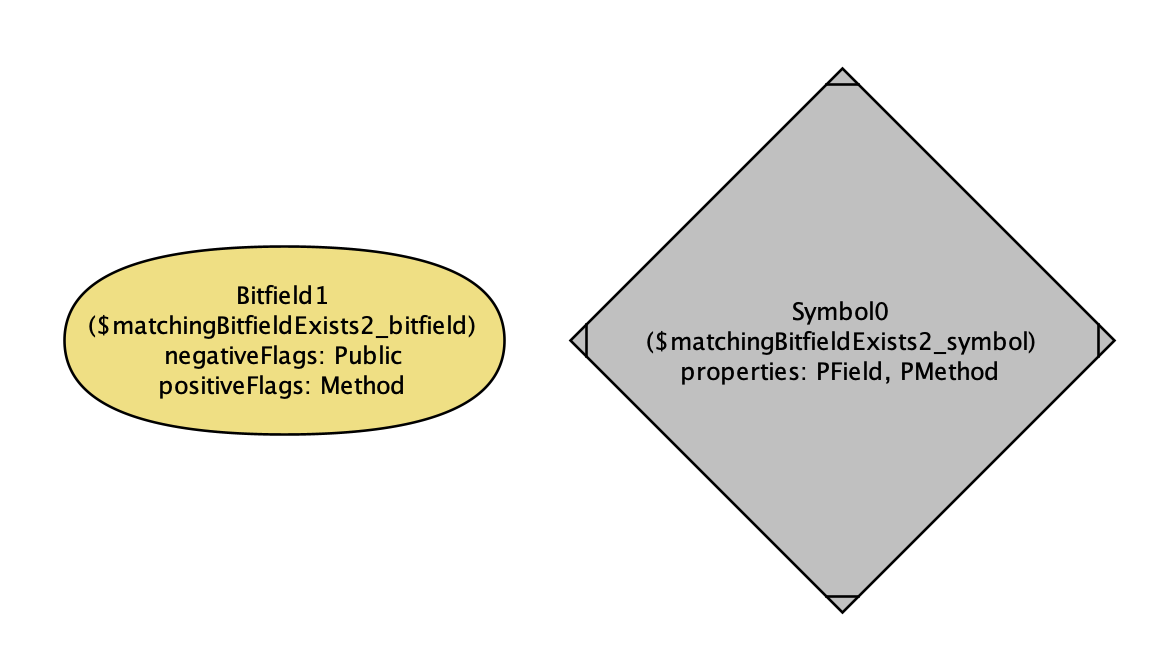
Alloy’s spiced up output satisfying “a bit field that matches a symbol exists”
We never told Alloy that a symbol can’t be both a field and a method. It
had no idea what the flags meant, just that they exist.
To let Alloy know what we do – that the two properties are incompatible –
we can use a fact. To me, the most natural way of phrasing this is “there
is never a symbol that has both the method and field properties”. Alas,
Alloy doesn’t have a never keyword; it only has always. So I opt instead
for an alternative formulation: “there are always zero symbols that are
both methods and fields”. In Alloy, the claim looks like this:
|
|
Re-running the example program with this fact, Alloy spits out a filter for public non-method symbols, and a symbol that’s a public field. Public fields also aren’t a thing in Chapel (all fields in a class are publicly readable in the current version of the language). Perhaps it’s time for another fact.
|
|
But now, Alloy fails to come up with anything at all. That makes sense: by
restricting the search to a symbol with two properties, and making PField
incompatible with the other two possible properties, we’ve guaranteed that
our symbol would be a public method. But then, we also required a negative
flag in the filter; however, all the flags in the list match a public
method, so making any of them negative would guarantee that our symbol
would not be found. Let’s change the example up a bit to only ask for
positive flags.
|
|
This time, Alloy gives us a symbol that’s a public method, and a filter that only looks for public methods. Fair enough.
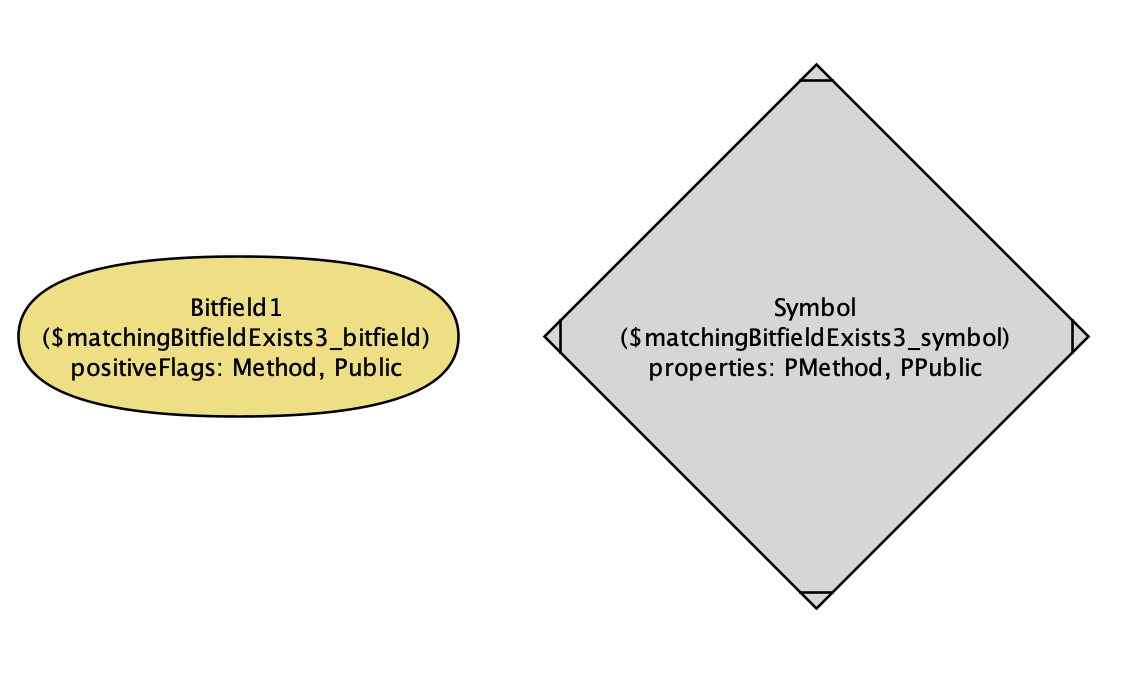
Alloy’s spiced up output satisfying “a bit field that matches a symbol exists”
Exploring Possible Search Configurations
So now we have a descriptioin of filters and symbols in scopes. The next thing on the itinerary is modeling how the filters (include and exclude) are configured during scope search in Dyno. For this, let’s take a look at the C++ code in Dyno.
I’ll be using the branch that I was working on at the time of trying to apply Alloy. First, here’s the code in C++ that defines the various flags I’d be working with (though I’ve omitted flags that are not currently used in the implementation).
enum {
/** Public */
PUBLIC = 1,
/** Not public (aka private) */
NOT_PUBLIC = 2,
/** A method or field declaration */
METHOD_FIELD = 4,
/** Something other than (a method or field declaration) */
NOT_METHOD_FIELD = 8,
/** A method declaration */
METHOD = 64,
/** Something other than a method declaration */
NOT_METHOD = 128,
};These are the flags that we model using a Bitset: PUBLIC,
METHOD_FIELD, and METHOD are modeled using positiveFlags, and
NOT_PUBLIC, NOT_METHOD_FIELD, and NOT_METHOD are modeled using
negativeFlags. There are a lot of flags here, and it’s not hard to
imagine that some combination of these flags will cause problems in our
system (particularly when we know it’s an approximation). However, the
flags aren’t used arbitrarily; in fact, it wasn’t too hard to track down the
most important place in the code where bitsets are built.
IdAndFlags::Flags curFilter = 0;
/* ... some unrelated code ... */
if (skipPrivateVisibilities) {
curFilter |= IdAndFlags::PUBLIC;
}
if (onlyMethodsFields) {
curFilter |= IdAndFlags::METHOD_FIELD;
} else if (!includeMethods && receiverScopes.empty()) {
curFilter |= IdAndFlags::NOT_METHOD;
}The above code converts the current search parameters into Bitfield
flags. For instance, if a use statement is being processed that doesn’t
have access to private fields, skipPrivateVisibilities will be set.
On the other hand, if the calling code didn’t explicitly ask for methods,
and if there’s no method receiver, then the last condition will be true.
These various conditions are converted into bits and applied to
curFilter. Then, curFilter is used for looking up symbols in a scope.
It’s not too hard to model this by just looking at the code, and
enumerating the possibilities. The first if statement can either be true
or false, and then the subsequent if-else chain creates three
possibilities in each case: either METHOD_FIELD is set, or NOT_METHOD,
or nothing.
However, I envisioned this condition to possibly grow in complexity as more
search configurations became necessary (in that, the NOT_METHOD option
was an addition in my new branch). I therefore chose to model the possible
Bitfield values more faithfully, by mimicking the imperative C++ code.
The essential piece of insight to modeling an imperative language, though
it sounds a little bit tautological, is that statements are all about
manipulating state. For example, state could be the value of a variable.
If you start with the variable x storing the number 6, and then execute
the statement x = x * 7, the final value of x will be 42. Thus, state
has changed. To put this in terms Alloy would understand – relations and
sets – a statement connects (relates) states before it’s executed to states
after it’s executed. In our particular example, the connection would
between the state x = 6 and the state x = 42. In the case of adding the
PUBLIC to curFilter, as on line 917 in the above code block, we could
state the relationship as follows:
addBitfieldFlag[bitfieldBefore, bitfieldAfter, Public]
The above code states that bitfieldAfter (the state after line 917) is
the same Bitfield as bitfieldBefore (the state before line 917), except
that the Public flag has been added to it.
Things are a little more complicated when it comes to modeling the whole
if-statement on line 916. If we wanted to be very precise, we’d need to
encode the other variables (such as skipPrivateVisibilities), how they’re
set, and what values are possible. However, for the sake of keeping the
scope of this model manageable for the time being, I’m content to do
something simpler – that is, acknowledge that the code on line 917 may or
may not run. If it does run, our previous addBitfieldFlag will be the
correct restriction on the before and after states. However, if it doesn’t,
the state shouldn’t change at all. Therefore, we can model lines 916
through 918 as follows (notice the or):
addBitfieldFlag[bitfieldBefore, bitfieldAfter, Public] or
bitfieldEqual[bitfieldBefore, bitfieldAfter]
The next thing to note is that there are two if statements one after another.
The state “after” the first statement is one and the same as the state
“before” the second statement. Using arrows to represent the “before-after”
relationship created by each statement, we can visualize the whole
situation as follows:
We’ll write our Alloy code to match:
/* First if statement */
addBitfieldFlag[bitfieldBefore, bitfieldMiddle, Public] or
bitfieldEqual[bitfieldBefore, bitfieldMiddle]
/* ... something connecting bitfieldMiddle and bitfieldAfter ... */
From here, we can handle the second if/else chain in the same way we
did the first if-statement: by making all three outcomes of the chain be
possible, and creating an or of all of them.
/* First if statement */
addBitfieldFlag[bitfieldBefore, bitfieldMiddle, Public] or
bitfieldEqual[bitfieldBefore, bitfieldMiddle]
/* Second if statement */
addBitfieldFlag[bitfieldMiddle, bitfieldAfter, MethodOrField] or
addBitfieldFlagNeg[bitfieldMiddle, bitfieldAfter, Method] or
bitfieldEqual[bitfieldMiddle, bitfieldAfter]
So that helps model the relevant Dyno code. However, what we really want is an Alloy predicate that classifies possible outcomes of the piece of code: is a particular combination of flags possible or not? Here’s the piece of Alloy that does so:
|
|
The FilterState on the first line (and elsewhere, really), is new. I’m
trying to be explicit about the state in this particular computation. Its
definition is very simple: currently, the only state we care about is the
Bitfield corresponding to curFilter in the C++ code above.
|
|
There’s not much more to the predicate. It says, in English, that a state
filterState is possible if, starting from an empty initial state
initialState, the model of our C++ code can end up with its particular
set of flags in the curFilter bitfield.
Modeling Search State
Next, I needed to model the behavior the I described earlier: searching for , and taking the intersection of past searches when running subsequent searches.
Dyno implemented this roughly as follows:
- It kept a mapping of (searched scope → search bitfield). Initially, this mapping was empty.
- When a scope was searched for the first time, its
curFilter/ search bitfield was stored into the mapping. - When a scope was searched after that, the previously-stored flags in the
mapping were excluded (that’s the behavior), and
the bitfield in the mapping was updated to be the intersection of
curFilterand the stored flags.
We’ll simplify the model by doing away with the mapping, and considering
only a single scope that is searched many times. We’ll represent the stored
flags as a field found, which will be one of two things: either a
Bitfield representing the previously-stored search configuration, or a
NotSet sentinel value, representing a scope that hasn’t been searched
yet. The Alloy code:
|
|
The NotSet sentinel value is defined in a very simple way:
|
|
Both of these signatures use a new keyword, one. This keyword means that
there’s only a single instance of both NotSet and SearchState in our
model. This is in contrast to a signature like Bitfield, which allows
multiple bitfields to exist at the same time. I ended up with a pretty
simple predicate that implemented the “store if not set, intersect if set”
behavior in Alloy:
|
|
If you look closely, this predicate uses a feature of Alloy we haven’t
really seen: its ability to reason about time by dipping into temporal logic.
Notice that the predicate is written not just in terms of toSet, but also
toSet'. The tick (which I personally read as “prime”) indicates that what
we’re talking about is not the current value of toSet, but its value at
the next moment in time.
The first line of the predicate represents the second item from the list
above: if a scope hasn’t been searched before (represented by the present
value of toSet being NotSet) the future value (represented by toSet')
is just the current filter / bitfield. The second line handles the third item
from the list, updating a previously-set filter based on new flags. I defined
an additional predicate to help with this:
|
|
What this predicate says is that at the next moment, the value of toSet
will be equal to its present value intersected with curFilter. I also had
to specify that the future value of toSet, will still be a
Bitfield after the step, and would not revert to a NotSet.
With the updateOrSet predicate in hand, we can actually specify how our
model will evolve. To do so, we first need to specify the initial
conditions. In particular, our scope will start out not having been
searched; its flags will be NotSet.
|
|
Next, we must specify that our SearchState changes in a very particular
way: each step, the code invokes a search, and the state is modified to
record that the search occurred. Each search is described via curFilter
in a filterState. We want to ensure that curFilter is a reasonable
filter (that is, it’s a combination of flags that can actually arise in the
C++ program). To ensure this, we can use the possibleState predicate from
earlier. From there, the updateOrSet predicate can be used to specify
that this step’s curFilter is saved, either as-is (if no searches
occurred previously) or as an intersection (if this is not the first
search). The whole fact corresponding to this is below:
|
|
Asking for Counterexamples
As we’ve already seen, Alloy works by finding examples: combinations of various variables that match our requirements. It won’t be sufficient to ask Alloy for an example of our code doing what we expect: if the code malfunctions nine times out of ten, Alloy will still find us the one case in which it works. It won’t tell us much.
Instead, we have to ask it to find a counterexample: a case which does not work. If Alloy succeeds in finding such an example, the code we’re modeling has a bug. Of course, to make all this work, you need to know what to ask. There’s no way to tell Alloy, “find me a bug” – we need to be more specific. I had to focus on bugs I was most worried about.
If the stored combination of flags (in found) evolves into a bad
configuration, things can go wrong in two ways. The first is that we will
somehow exclude symbols from the lookup that shouldn’t have been excluded.
In other words, can past searches break future searches?
I came up with the following Alloy (counter)example to model this situation. It’s a little bit long; there are comments there to explain what it does, and I’ll go through below.
|
|
This example asks that at some point in time, things “go wrong”. In
particular, will there by a symbol (symbol) that hasn’t been found yet,
such that a search for a particular filter (fs) will break the system,
making a subsequent search fsBroken not find symbol even though it
should have?
The possibleState, updateOrSet, and excludeBitfield
lines encode the fact that a search occurred for fs. This must be a valid
search, and the search state must be modified appropriately. Furthermore,
at the time this search takes place, to make the portion of
the algorithm work, the bitfield exclude1 will be set based on the
previous search state.
The next two lines, possibleState and excludeBitfield, set the stage for
the broken search: fsBroken is a another valid search, and at the time it
happens, the bitfield exclude2 is set based on previous search state.
Since fsBroken occurs after fs, its “previous search state” is actually
the state after fs, so we use found' instead of found.
Finally, the subsequent four lines of code describe the issue: the symbol
in question has not been found before fs, and nor will it be found by
fs. That means thus far, it hasn’t been reported to the user.
Therefore, if the symbol matches fsBroken, it ought to be reported: we haven’t
seen it yet, and here we’re being asked for something matching the symbol’s
description! However, as per the last line of code, searching for
fsBroken together with the appropriate set of exclude flags, we still
don’t find symbol. That’s a problem!
Unfortunately, Alloy finds a model that satisfies this constraint. There are a lot of moving parts, so the output is a bit difficult to read. I did my best to clean it up by turning off some arrows. Our system is spanning multiple “moments” in time, so a single picture won’t describe the bug entirely. Here’s the diagram Alloy outputs for the first state:
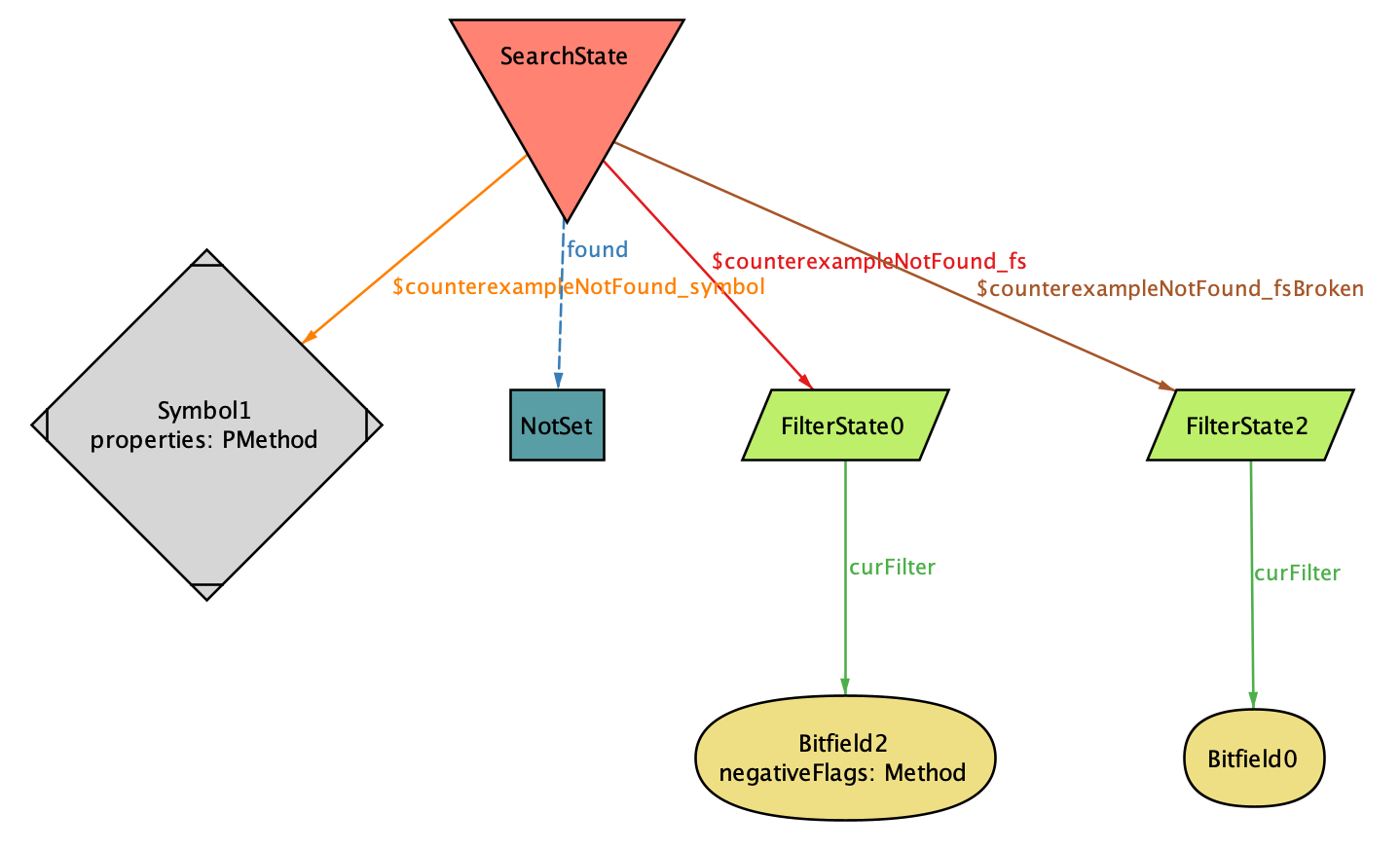
Figure representing the initial state according to Alloy
We can get a lot out of this figure. First, the symbol-to-be-lost is a
private method (it doesn’t have the PPublic property, and it does have
the PMethod property). Also, Alloy immediately gives away what fs and
fsBroken will be: eventually, when the user searches for all
non-methods (negativeFlags: Method are the giveaway there), their
subsequent search for anything will fail to come up with our private
method, even though it should. To gather more details about this broken
case, we can look at the state that follows the initial one.
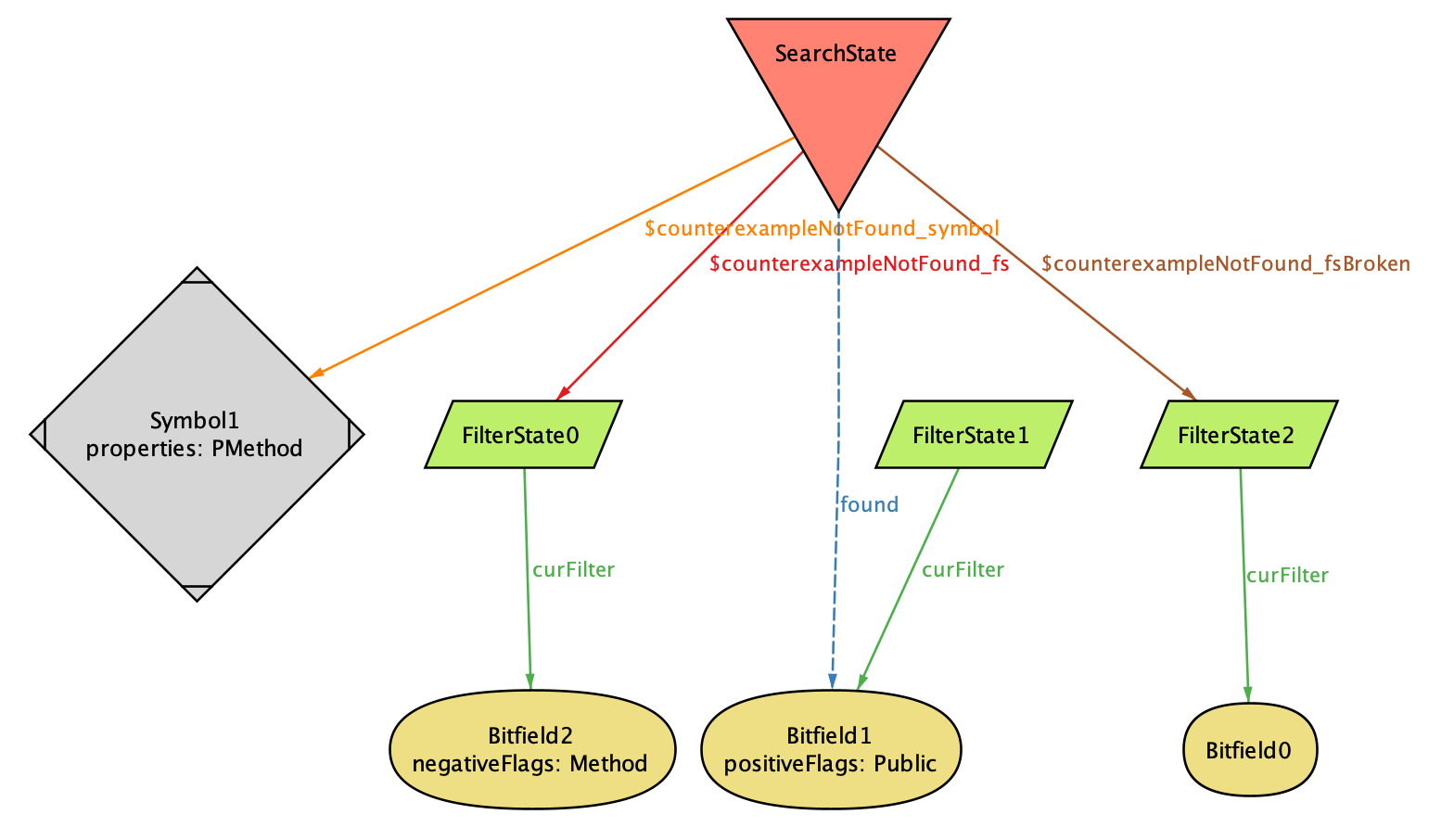
Figure representing the second state according to Alloy
The main difference is that found has changed from NotSet (because no
searches occurred) to FilterState1. This indicates that the first search
was for all Public symbols (which our method is not). There is only one
more state after this:
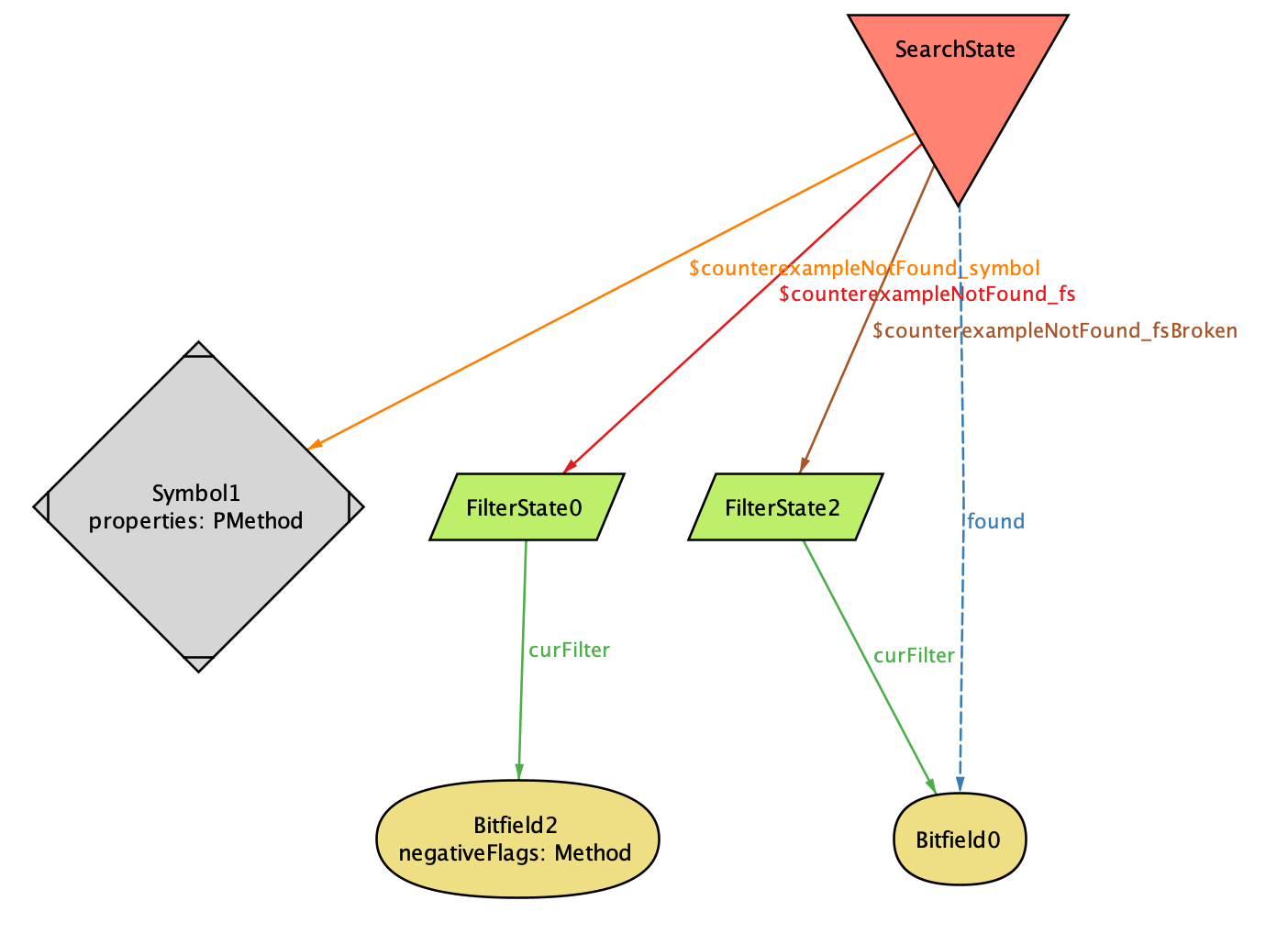
Figure representing the final state according to Alloy
In the above diagram, found has changed once again, this time to an empty
bitfield. This is a valid behavior for our system. Recall that fs was a
search for non-methods, and that the intersection of NOT_METHOD and PUBLIC
is empty. Thus, found will be set to the empty bitfield, which
(incorrectly) indicates that all symbols have been searched for! After
this, any search would fail: fsBroken doesn’t have any flags set, and
still, nothing is reported.
Now, this doesn’t definitively prove the compiler is broken: it’s possible
that there isn’t a situation in which three searches like this (PUBLIC,
then NOT_METHOD, then anything) will occur in practice. However, this
gave the “motif” for reproducing the bug. All I had to do was find a
real-life case that matched the counterexample.
It was a little easier to find a reproducer for a similar counterexample,
actually. By inspection, I noticed that the same bug would occur if the
second search was for METHOD_OR_FIELD, and not for NOT_METHOD. I was
able to come up with a (fairly convoluted) example of Chapel code that
triggered the issue. I include it here as a curiosity; there’s no need to
understand how exactly it works.
module TopLevel {
module XContainerUser {
public use TopLevel.XContainer; // Will search for public, to no avail.
}
module XContainer {
private var x: int;
record R {} // R is in the same scope as x so it won't set public
module MethodHaver {
use TopLevel.XContainerUser;
use TopLevel.XContainer;
proc R.foo() {
var y = x;
}
}
}
}
Alas, the two-bitfield system is not just an approximation, it malfunctions in practice. I submitted a PR to fix the issue.