Earlier, I wrote an article in which I used Coq to encode the formal semantics of Dawn’s Untyped Concatenative Calculus, and to prove a few things about the mini-language. Though I’m quite happy with how that turned out, my article was missing something that’s present on the original Dawn page – an evaluator. In this article, I’ll define an evaluator function in Coq, prove that it’s equivalent to Dawn’s formal semantics, and extract all of this into usable Haskell code.
Changes Since Last Time
In trying to write and verify this evaluator, I decided to make changes to the way I formalized
the UCC. Remember how we used a predicate, IsValue, to tag expressions that were values?
It turns out that this is a very cumbersome approach. For one thing, this formalization
allows for the case in which the exact same expression is a value for two different
reasons. Although IsValue has only one constructor (Val_quote), it’s actually
[note:
Interestingly, it's also not provable that any two proofs of are equal,
even though equality only has one constructor, .
Under the homotopic interpretation
of type theory, this corresponds to the fact that two paths from to need
not be homotopic (continuously deformable) to each other.
As an intuitive example, imagine wrapping a string around a pole. Holding the ends of
the string in place, there's nothing you can do to "unwrap" the string. This string
is thus not deformable into a string that starts and stops at the same points,
but does not go around the pole.
]
that any two proofs of IsValue e are equal. I ended up getting into a lot of losing
arguments with the Coq runtime about whether or not two stacks are actually the same.
Also, some of the semantic rules expected a value on the stack with a particular proof
for IsValue, and rejected the exact same stack with a generic value.
Thus, I switched from our old implementation:
|
|
To the one I originally had in mind:
|
|
I then had the following function to convert a value back into an equivalent expression:
|
|
I replaced instances of projT1 with instances of value_to_expr.
Where We Are
At the end of my previous article, we ended up with a Coq encoding of the big-step operational semantics of UCC, as well as some proofs of correctness about the derived forms from the article (like and ). The trouble is, despite having our operational semantics, we can’t make our Coq code run anything. This is for several reasons:
- Our definitions only let us to confirm that given some
initial stack, a program ends up in some other final stack. We even have a
little
Ltac2tactic to help us automate this kind of proof. However, in an evaluator, the final stack is not known until the program finishes running. We can’t confirm the result of evaluation, we need to find it. - To address the first point, we could try write a function that takes a program and an initial stack, and produces a final stack, as well as a proof that the program would evaluate to this stack under our semantics. However, it’s quite easy to write a non-terminating UCC program, whereas functions in Coq have to terminate! We can’t write a terminating function to run non-terminating code.
So, is there anything we can do? No, there isn’t. Writing an evaluator in Coq is just not possible. The end, thank you for reading.
Just kidding – there’s definitely a way to get our code evaluating, but it will look a little bit strange.
A Step-by-Step Evaluator
The trick is to recognize that program evaluation occurs in steps. There may well be an infinite number of steps, if the program is non-terminating, but there’s always a step we can take. That is, unless an invalid instruction is run, like trying to clone from an empty stack, or unless the program finished running. You don’t need a non-terminating function to just give you a next step, if one exists. We can write such a function in Coq.
Here’s a new data type that encodes the three situations we mentioned in the previous paragraph. Its constructors (one per case) are as follows:
-
err- there are no possible evaluation steps due to an error. -
middle e s- the evaluation took a step; the stack changed tos, and the rest of the program ise. -
final s- there are no possible evaluation steps because the evaluation is complete, leaving a final stacks.
|
|
We can now write a function that tries to execute a single step given an expression.
|
|
Most intrinsics, by themselves, complete after just one step. For instance, a program consisting solely of will either fail (if the stack doesn’t have enough values), or it will swap the top two values and be done. We list only “correct” cases, and resort to a “catch-all” case on line 26 that returns an error. The one multi-step intrinsic is , which can evaluate an arbitrary expression from the stack. In this case, the “one step” consists of popping the quoted value from the stack; the “remaining program” is precisely the expression that was popped.
Quoting an expression also always completes in one step (it simply places the quoted
expression on the stack). The really interesting case is composition. Expressions
are evaluated left-to-right, so we first determine what kind of step the left expression (e1)
can take. We may need more than one step to finish up with e1, so there’s a good chance it
returns a “rest program” e1' and a stack vs'. If this happens, to complete evaluation of
, we need to first finish evaluating , and then evaluate .
Thus, the “rest of the program” is , or e_comp e1' e2. On the other hand,
if e1 finished evaluating, we still need to evaluate e2, so our “rest of the program”
is , or e2. If evaluating e1 led to an error, then so did evaluating e_comp e1 e2,
and we return err.
Extracting Code
Just knowing a single step is not enough to run the code. We need something that repeatedly tries to take a step, as long as it’s possible. However, this part is once again not possible in Coq, as it brings back the possibility of non-termination. So if we can’t use Coq, why don’t we use another language? Coq’s extraction mechanism allows us to do just that.
I added the following code to the end of my file:
|
|
Coq happily produces a new file, UccGen.hs with a lot of code. It’s not exactly the most
aesthetic; here’s a quick peek:
data Intrinsic =
Swap
| Clone
| Drop
| Quote
| Compose
| Apply
data Expr =
E_int Intrinsic
| E_quote Expr
| E_comp Expr Expr
data Value =
V_quote Expr
-- ... more
All that’s left is to make a new file, Ucc.hs. I use a different file so that
Coq doesn’t overwrite my changes every time I re-run extraction. In this
file, we place the “glue code” that tries running one step after another:
|
|
Finally, loading up GHCi using ghci Ucc.hs, I can run the following commands:
ghci> fromList = foldl1 E_comp
ghci> test = eval [] $ fromList [true, false, UccGen.or]
ghci> :f test
test = Just [V_quote (E_comp (E_int Swap) (E_int Drop))]
That is, applying or to true and false results a stack with only true on top.
As expected, and proven by our semantics!
Proving Equivalence
Okay, so true false or evaluates to true, much like our semantics claims.
However, does our evaluator always match the semantics? So far, we have not
claimed or verified that it does. Let’s try giving it a shot.
First Steps and Evaluation Chains
The first thing we can do is show that if we have a proof that e takes
initial stack vs to final stack vs', then each
eval_step “makes progress” towards vs' (it doesn’t simply return
vs', since it only takes a single step and doesn’t always complete
the evaluation). We also want to show that if the semantics dictates
e finishes in stack vs', then eval_step will never return an error.
Thus, we have two possibilities:
-
eval_stepreturnsfinal. In this case, for it to match our semantics, the final stack must be the same asvs'. Here’s the relevant section from the Coq file:From DawnEval.v, line 3030(eval_step vs e = final vs') \/ -
eval_stepreturnsmiddle. In this case, the “rest of the program” needs to evaluate tovs'according to our semantics (otherwise, taking a step has changed the program’s final outcome, which should not happen). We need to quantify the new variables (specifically, the “rest of the program”, which we’ll callei, and the “stack after one step”,vsi), for which we use Coq’sexistsclause. The whole relevant statement is as follows:From DawnEval.v, lines 31 through 3331 32 33(exists (ei : expr) (vsi : value_stack), eval_step vs e = middle ei vsi /\ Sem_expr vsi ei vs').
The whole theorem statement is as follows:
|
|
I have the Coq proof script for this (in fact, you can click the link
at the top of the code block to view the original source file). However,
there’s something unsatisfying about this statement. In particular,
how do we prove that an entire sequence of steps evaluates
to something? We’d have to examine the first step, checking if
it’s a “final” step or a “middle” step; if it’s a “middle” step,
we’d have to move on to the “rest of the program” and repeat the process.
Each time we’d have to “retrieve” ei and vsi from eval_step_correct,
and feed it back to eval_step.
I’ll do you one better: how do we even say that an expression “evaluates
step-by-step to final stack vs'”? For one step, we can say:
eval_step vs e = final vs'
Here’s a picture so you can start visualizing what it looks like. The black line represents a single “step”.

Visual representation of a single-step evaluation.
For two steps, we’d have to assert the existence of an intermediate expression (the “rest of the program” after the first step):
exists ei vsi,
eval_step vs e = middle ei vsi /\ (* First step to intermediate expression. *)
eval_step vsi ei = final vs' (* Second step to final state. *)
Once again, here’s a picture. I’ve highlighted the intermediate state, Visual representation of a two-step evaluation.vsi, in
a brighter color.

For three steps:
exists ei1 ei2 vsi1 vsi2,
eval_step vs e = middle ei1 vsi1 /\ (* First step to intermediate expression. *)
eval_step vsi1 ei1 = middle ei2 vsi2 /\ (* Second intermediate step *)
eval_step vsi2 ei2 = final vs' (* Second step to final state. *)
I can imagine that you’re getting the idea, but here’s one last picture:
Visual representation of a three-step evaluation.
The Coq code for this is awful! Not only is this a lot of writing, but it also makes various
sequences of steps have a different “shape”. This way, we can’t make
proofs about evaluations of an arbitrary number of steps. Not all is lost, though: if we squint
a little at the last example (three steps), a pattern starts to emerge.
First, let’s re-arrange the exists quantifiers:
exists ei1 vsi1, eval_step vs e = middle ei1 vsi1 /\ (* Cons *)
exists ei2 vsi2, eval_step vsi1 ei1 = middle ei2 vsi2 /\ (* Cons *)
eval_step vsi2 ei2 = final vs' (* Nil *)
If you squint at this, it kind of looks like a list! The “empty” part of a list is the final step, while the “cons” part is a middle step. The analogy holds up for another reason: an “empty” sequence has zero intermediate expressions, while each “cons” introduces a single new intermediate program.
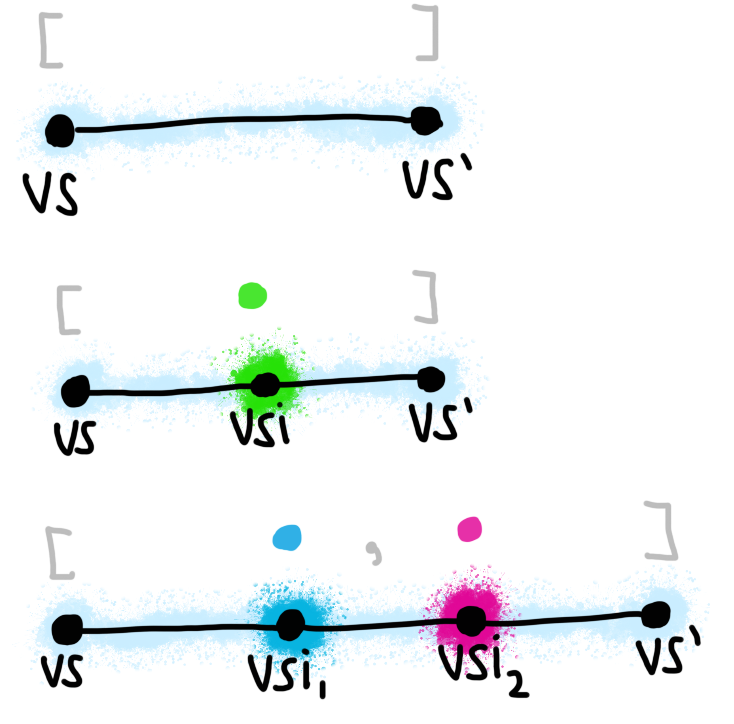
Evaluation sequences as lists.
Perhaps we can define a new data type that matches this? Indeed we can!
|
|
The new data type is parameterized by the initial and final stacks, as well as the expression that starts in the former and ends in the latter. Then, consider the following type:
eval_chain nil (e_comp (e_comp true false) or) (true :: nil)
This is the type of sequences (or chains) of steps corresponding to the
evaluation of the program ,
starting in an empty stack and evaluating to a stack with only
on top. Thus to say that an expression evaluates to some
final stack vs', in some unknown number of steps, it’s sufficient to write:
eval_chain vs e vs'
Evaluation chains have a couple of interesting properties. First and foremost,
they can be “concatenated”. This is analogous to the Sem_e_comp rule
in our original semantics: if an expression e1 starts in stack vs
and finishes in stack vs', and another expression starts in stack vs'
and finishes in stack vs'', then we can compose these two expressions,
and the result will start in vs and finish in vs''.
|
|
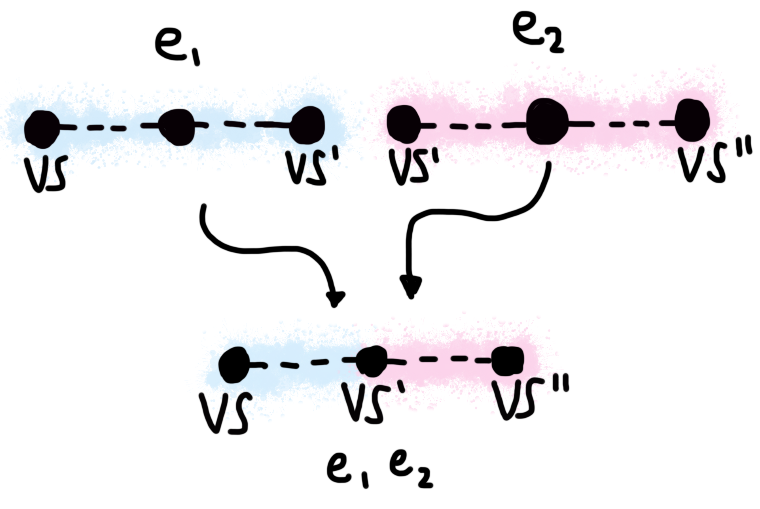
Merging evaluation chains.
The proof is very short. We go
[note:
It's not a coincidence that defining something like (++)
(list concatenation) in Haskell typically starts by pattern matching
on the left list. In fact, proofs by induction
actually correspond to recursive functions! It's tough putting code blocks
in sidenotes, but if you're playing with the
DawnEval.v file, try running
Print eval_chain_ind, and note the presence of fix,
the fixed point
combinator used to implement recursion.
]
(the one for e1). Coq takes care of most of the rest with auto.
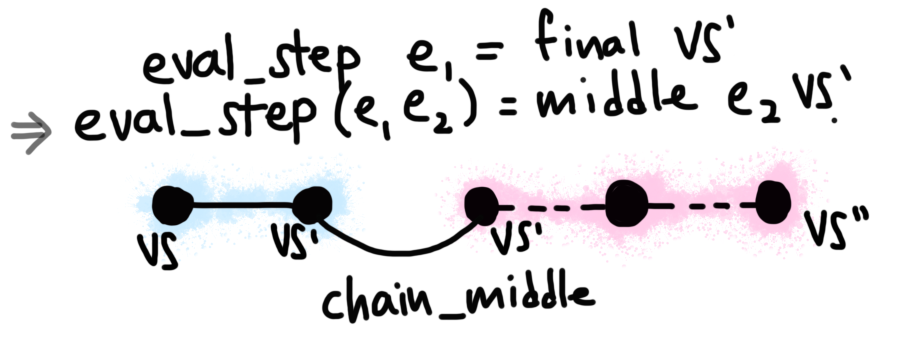
The key to this proof is that whatever P is contained within a “node”
in the left chain determines how eval_step (e_comp e1 e2) behaves. Whether
e1 evaluates to final or middle, the composition evaluates to middle
(a composition of two expressions cannot be done in one step), so we always
[note:
This is unlike list concatenation, since we typically don't
create new nodes when appending to an empty list.
]
via chain_middle. Then, the two cases are as follows.
If the step was Merging evaluation chains when the first chain only has one step.final, then
the rest of the steps use only e2, and good news, we already have a chain
for that!
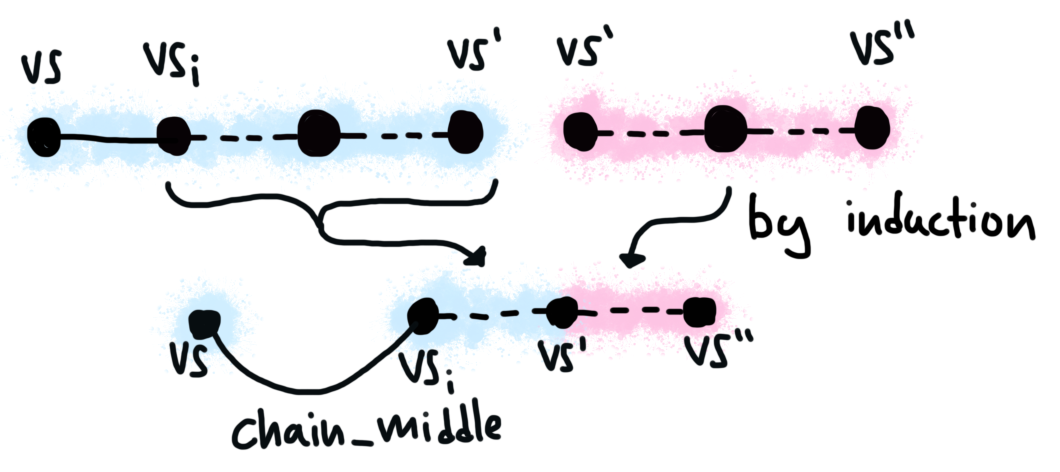
Otherwise, the step was Merging evaluation chains when the first chain has a middle step and others.middle, an we still have a chain for some
intermediate program ei that starts in some stack vsi and ends in vs'.
By induction, we know that this chain can be concatenated with the one
for e2, resulting in a chain for e_comp ei e2. All that remains is to
attach to this sub-chain the one step from (vs, e1) to (vsi, ei), which
is handled by chain_middle.
The merge operation is reversible; chains can be split into two pieces,
one for each composed expression:
|
|
While interesting, this particular fact isn’t used anywhere else in this post, and I will omit the proof here.
The Forward Direction
Let’s try rewording our very first proof, eval_step_correct, using
chains. The direction remains the same: given that an expression
produces a final stack under the formal semantics, we need to
prove that this expression evaluates to the same final stack using
a sequence of eval_step.
|
|
The power of this theorem is roughly the same as that of
the original one: we can use eval_step_correct to build up a chain
by applying it over and over, and we can take the “first element”
of a chain to serve as a witness for eval_step_correct. However,
the formulation is arguably significantly cleaner, and contains
a proof for all steps right away, rather than a single one.
Before we go through the proof, notice that there’s actually two
theorems being stated here, which depend on each other. This
is not surprising given that our semantics are given using two
data types, Sem_expr and Sem_int, each of which contains the other.
Regular proofs by induction, which work on only one of the data types,
break down because we can’t make claims “by induction” about the other
type. For example, while going by induction on Sem_expr, we run into
issues in the e_int case while handling . We know
a single step – popping the value being run from the stack. But what then?
The rule for in Sem_int contains another Sem_expr
which confirms that the quoted value properly evaluates. But this other
Sem_expr isn’t directly a child of the “bigger” Sem_expr, and so we
don’t get an inductive hypothesis about it. We know nothing about it; we’re stuck.
We therefore have two theorems declared together using with (just like we
used with to declare Sem_expr and Sem_int). We have to prove both,
which is once again a surprisingly easy task thanks to Coq’s auto. Let’s
start with the first theorem, the one for expression semantics.
|
|
We go by induction on the semantics data type. There are therefore three cases:
intrinsics, quotes, and composition. The intrinsic case is handed right
off to the second theorem (which we’ll see momentarily). The quote case
is very simple since quoted expressions are simply pushed onto the stack in
a single step (we thus use chain_final). Finally, in the composition
case, we have two sub-proofs, one for each expression being evaluated.
By induction, we know that each of these sub-proofs can be turned into
a chain, and we use eval_chain_merge to combine these two chains into one.
That’s it.
Now, let’s try the second theorem. The code is even shorter:
|
|
The first command, inversion Hsem, lets us go case-by-case on the various
ways an intrinsic can be evaluated. Most intrinsics are quite boring;
in our evaluator, they only need a single step, and their semantics
rules guarantee that the stack has the exact kind of data that the evaluator
expects. We dismiss such cases with apply chain_final; auto. The only
time this doesn’t work is when we encounter the intrinsic;
in that case, however, we can simply use the first theorem we proved.
A Quick Aside: Automation Using Ltac2
Going in the other direction will involve lots of situations in which we know
that eval_step evaluated to something. Here’s a toy proof built around
one such case:
|
|
The proof claims that if the swap instruction was evaluated to something,
then the initial stack must contain two values, and the final stack must
have those two values on top but flipped. This is very easy to prove, since
that’s the exact behavior of eval_step for the swap intrinsic. However,
notice how much boilerplate we’re writing: lines 241 through 244 deal entirely
with ensuring that our stack does, indeed, have two values. This is trivially true:
if the stack didn’t have two values, it wouldn’t evaluate to final, but to error.
However, it takes some effort to convince Coq of this.
This was just for a single intrinsic. What if we’re trying to prove something
for every intrinsic? Things will get messy very quickly. We can’t even re-use
our destruct vs code, because different intrinsics need stacks with different numbers
of values (they have a different arity); if we try to handle all cases with at most
2 values on the stack, we’d have to prove the same thing twice for simpler intrinsics.
In short, proofs will look like a mess.
Things don’t have to be this way, though! The boilerplate code is very repetitive, and
this makes it a good candidate for automation. For this, Coq has Ltac2.
In short, Ltac2 is another mini-language contained within Coq. We can use it to put
into code the decision making that we’d be otherwise doing on our own. For example,
here’s a tactic that checks if the current proof has a hypothesis in which
an intrinsic is evaluated to something:
|
|
Ltac2 has a pattern matching construct much like Coq itself does, but it can
pattern match on Coq expressions and proof goals. When pattern matching
on goals, we use the following notation: [ h1 : t1, ..., hn : tn |- g ], which reads:
Given hypotheses
h1throughhn, of typest1throughtnrespectively, we need to proveg.
In our pattern match, then, we’re ignoring the actual thing we’re supposed to prove
(the tactic we’re writing won’t be that smart; its user – ourselves – will need
to know when to use it). We are, however, searching for a hypothesis in the form
eval_step ?a (e_int ?b) = ?c. The three variables, ?a, ?b, and ?c are placeholders
which can be matched with anything. Thus, we expect any hypothesis in which
an intrinsic is evaluated to anything else (by the way, Coq checks all hypotheses one-by-one,
starting at the most recent and finishing with the oldest). The code on lines 144 through 146 actually
performs the destruct calls, as well as the inversion attempts that complete
any proofs with an inconsistent assumption (like err = final vs').
So how do these lines work? Well, first we need to get a handle on the hypothesis we found.
Various tactics can manipulate the proof state, and cause hypotheses to disappear;
by calling Control.hyp on h, we secure a more permanent hold on our evaluation assumption.
In the next line, we call another Ltac2 function, destruct_int_stack, which unpacks
the stack exactly as many times as necessary. We’ll look at this function in a moment.
Finally, we use regular old tactics. Specifically, we use inversion (as mentioned before).
I use fail after inversion to avoid cluttering the proof in case there’s not
a contradiction.
On to destruct_int_stack. The definition is very simple:
|
|
The main novelty is that this function takes two arguments, both of which are Coq expressions:
int, or the intrinsic being evaluated, and va, the stack that’s being analyzed. The constr
type in Coq holds terms. Let’s look at int_arity next:
|
|
This is a pretty standard pattern match that assigns to each expression its arity. However, we’re
case analyzing over literally any possible Coq expression, so we need to handle the case in which
the expression isn’t actually a specific intrinsic. For this, we use Control.throw with
the Not_intrinsic exception.
Wait a moment, does Coq just happen to include a Not_intrinsic exception? No, it does not.
We have to register that one ourselves. In Ltac2, the type of exception (exn) is extensible,
which means we can add on to it. We add just a single constructor with no arguments:
|
|
Finally, unpacking the value stack. Here’s the code for that:
|
|
This function accepts the arity of an operation, and unpacks the stack that many times.
Ltac2 doesn’t have a way to pattern match on numbers, so we resort to good old “less than or equal”,
and and if/else. If the arity is zero (or less than zero, since it’s an integer), we don’t
need to unpack anymore. This is our base case. Otherwise, we generate two new free variables
(we can’t just hardcode v1 and v2, since they may be in use elsewhere in the proof). To this
end we use Fresh.in_goal and give it a “base symbol” to build on. We then use
destruct, passing it our “scrutinee” (the expression being destructed) and the names
we generated for its components. This generates multiple goals; the Control.enter tactic
is used to run code for each one of these goals. In the non-empty list case, we try to break
apart its tail as necessary by recursively calling destruct_n.
That’s pretty much it! We can now use our tactic from Coq like any other. Rewriting our earlier proof about , we now only need to handle the valid case:
|
|
We’ll be using this new ensure_valid_stack tactic in our subsequent proofs.
The Backward Direction
After our last proof before the Ltac2 diversion, we know that our evaluator matches our semantics, but only when a Sem_expr
object exists for our program. However, invalid programs don’t have a Sem_expr object
(there’s no way to prove that they evaluate to anything). Does our evaluator behave
properly on “bad” programs, too? We’ve not ruled out that our evaluator produces junk
final or middle outputs whenever it encounters an error. We need another theorem:
|
|
That is, if our evalutor reaches a final state, this state matches our semantics. This proof is most conveniently split into two pieces. The first piece says that if our evaluator completes in a single step, then this step matches our semantics.
|
|
The statement for a non-final step is more involved; the one step by itself need
not match the semantics, since it only carries out a part of a computation. However,
we can say that if the “rest of the program” matches the semantics, then so does
the whole expression.
|
|
Finally, we snap these two pieces together in eval_step_sem_back:
|
|
We have now proved complete equivalence: our evaluator completes in a final state
if and only if our semantics lead to this same final state. As a corollary of this,
we can see that if a program is invalid (it doesn’t evaluate to anything under our semantics),
then our evaluator won’t finish in a final state:
|
|
Making a Mini-REPL
We can now be pretty confident about our evaluator. However, this whole business with using GHCi
to run our programs is rather inconvenient; I’d rather write [drop] than E_quote (E_int Drop).
I’d also rather read the former instead of the latter. We can do some work in Haskell to make
playing with our interpreter more convenient.
Pretty Printing Code
Coq generated Haskell data types that correspond precisely to the data types we defined for our proofs. We can use the standard type class mechanism in Haskell to define how they should be printed:
|
|
Now our expressions and values print a lot nicer:
ghci> true
[swap drop]
ghci> false
[drop]
ghci> UccGen.or
clone apply
Reading Code In
The Parsec library in Haskell can be used to convert text back into data structures. It’s not too hard to create a parser for UCC:
|
|
Now, parseExpression can be used to read code:
ghci> parseExpression "[drop] [drop]"
Right [drop] [drop]
The REPL
We now literally have the three pieces of a read-evaluate-print loop. All that’s left is putting them together:
|
|
We now have our own little verified evaluator:
$ ghci Ucc
$ ghc -main-is Ucc Ucc
$ ./Ucc
> [drop] [drop] clone apply
[[drop]]
> [drop] [swap drop] clone apply
[[swap drop]]
> [swap drop] [drop] clone apply
[[swap drop]]
> [swap drop] [swap drop] clone apply
[[swap drop]]
Potential Future Work
We now have a verified UCC evaluator in Haskell. What next?
-
We only verified the evaluation component of our REPL. In fact, the whole thing is technically a bit buggy due to the parser:
> [drop] drop coq is a weird name to say out loud in interviews []Shouldn’t this be an error? Do you see why it’s not? There’s work in writing formally verified parsers; some time ago I saw a Galois talk about a formally verified parser generator. We could use this formally verified parser generator to create our parsers, and then be sure that our grammar is precisely followed.
-
We could try make our evaluator a bit smarter. One thing we could definitely do is maker our REPL support variables. Then, we would be able to write:
> true = [swap drop] > false = [drop] > or = clone apply > true false or [swap drop]There are different ways to go about this. One way is to extend our
exprdata type with a variable constructor. This would complicate the semantics (a lot), but it would allow us to prove facts about variables. Alternatively, we could implement expressions as syntax sugar in our parser. Using a variable would be the same as simply pasting in the variable’s definition. This is pretty much what the Dawn article seems to be doing. -
We could prove more things. Can we confirm, once and for all, the correctness of , for any ? Is there is a generalized way of converting inductive data types into a UCC encoding? Or could we perhaps formally verify the following comment from Lobsters:
with the encoding of natural numbers given, n+1 contains the definition of n duplicated two times. This means that the encoding of n has size exponential in n, which seems extremely impractical.
The world’s our oyster!
Despite all of these exciting possibilities, this is where I stop, for now. I hope you enjoyed this article, and thank you for reading!