Inference Rules and the Study of Programming Languages
In this post, I will talk about inference rules, particularly in the field of programming language theory. The first question to get out of the way is “what on earth is an inference rule?”. The answer is simple: an inference rule is just a way of writing “if … then …”. When writing an inference rule, we write the “if” stuff above a line, and the “then” stuff below the line. Really, that’s all there is to it. I’ll steal an example from another one of my posts on the blog – here’s an inference rule:
We can read this as “if I’m allergic to cats, and my friend has a cat, then I will not visit my friend very much”.
In the field of programming languages, inference rules are everywhere. Practically any paper I read has a table that looks something like this:

Inference rules from Logarithm and program testing by Kuen-Bang Hou (Favonia) and Zhuyang Wang
And I, for one, love it! They’re a precise and concise way to describe static and dynamic behavior of programs. I might’ve written this elsewhere on the blog, but whenever I read a paper, my eyes search for the rules first and foremost.
But to those just starting their PL journey, inference rules can be quite cryptic – I know they were to me! The first level of difficulty are the symbols: we have lots of Greek ( and for environments, and perhaps for types), and the occasional mathematical symbol (the “entails” symbol is the most common, but for operational semantics we can have and ). If you don’t know what they mean, or if you’re still getting used to them, symbols in judgements are difficult enough to parse.
The second level of difficulty is making sense of the individual rules: although they tend to not be too bad, for some languages even making sense of one rule can be challenging. The following rule from the Calculus of Inductive Constructions is a doozy, for instance.
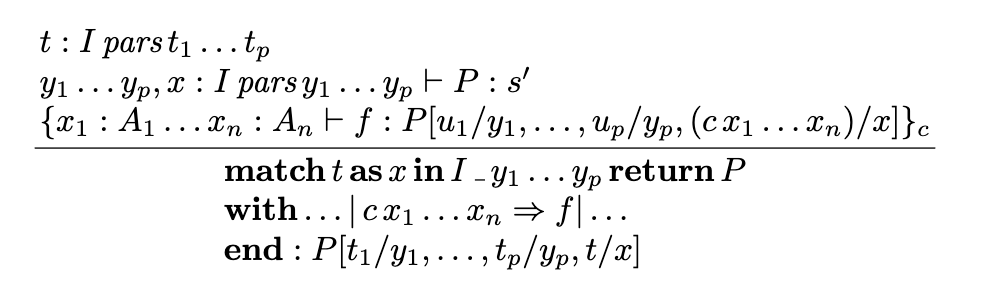
The match inference rule from Introduction to the Calculus of Inductive Constructions by Christine Paulin-Mohring
Just look at the metavariables! We have , through , through , plain , and at least two other sets of variables. Not only this, but the rule requires at least some familiarity with GADTs to understand completely.
The third level is making sense of how the rules work, together. In my programming languages class in college, a familiar question was:
the Hindley-Milner type system supports let-polymorphism only. What is it about the rules that implies let-polymorphism, and not any other kind of polymorphism?
If you don’t know the answer, or the question doesn’t make sense do you, don’t worry about it – suffice to say that whole systems of inference rules exhibit certain behaviors, and it takes familiarity with several rules to spot these behaviors.
Seeing What Works and What Doesn’t
Maybe I’m just a tinker-y sort of person, but for me, teaching inference rules just by showing them is not really enough. For instance, let me show you two ways of writing the following (informal) rule:
When adding two operands, if both operands are strings, then the result of adding them is also a string.
There’s a right way to write this inference rule, and there is a wrong way. Let me show you both, and try to explain the two. First, here’s the wrong way:
This says that the type of adding two variables of type string is still string.
Here, is a context, which keeps track of which variable has what
type. Writing is the same as saying
“we know the variable x has type string”. The whole rule reads,
If the variables
xandyboth have typestring, then the result of adding these two variables,x+y, also has typestring.
The trouble with this rule is that it only works when adding two variables.
But x+x is not itself a variable, so the rule wouldn’t work for an expression
like (x+x)+(y+y). The proper way of writing the rule is, then, something like
this:
This rule says:
If the two subexpressions
e1ande2both have typestring, then the result of adding these two subexpressions,e1+e2, also has typestring.
Much better! We can apply this rule recursively: to get the type of (x+x)+(y+y),
we consider (x+x) and (y+y) as two subexpressions, and go on to compute
their types first. We can then break (x+x) into two subexpressions (x and x),
and determine their type separately. Supposing that the variables x and y
indeed have the type string, this tells us that (x+x) and (y+y) are both
string, and therefore that the whole of (x+x)+(y+y) is a string.
What I’d really like to do is type the program in question and have the computer figure out whether my rules accept or reject this program. With my new rules, perhaps I’d get something like this:

Verifying the (x+x)+(y+y) expression using the good rule
To fully understand how the rule works to check a big expression like the above
sum, I’d need to see the recursion we applied a couple of paragraphs ago. My
ideal tool would display this too. For simplicity, I’ll just show the output
for (1+1)+(1+1), sidestepping variables and using numbers instead. This just
saves a little bit of space and visual noise.
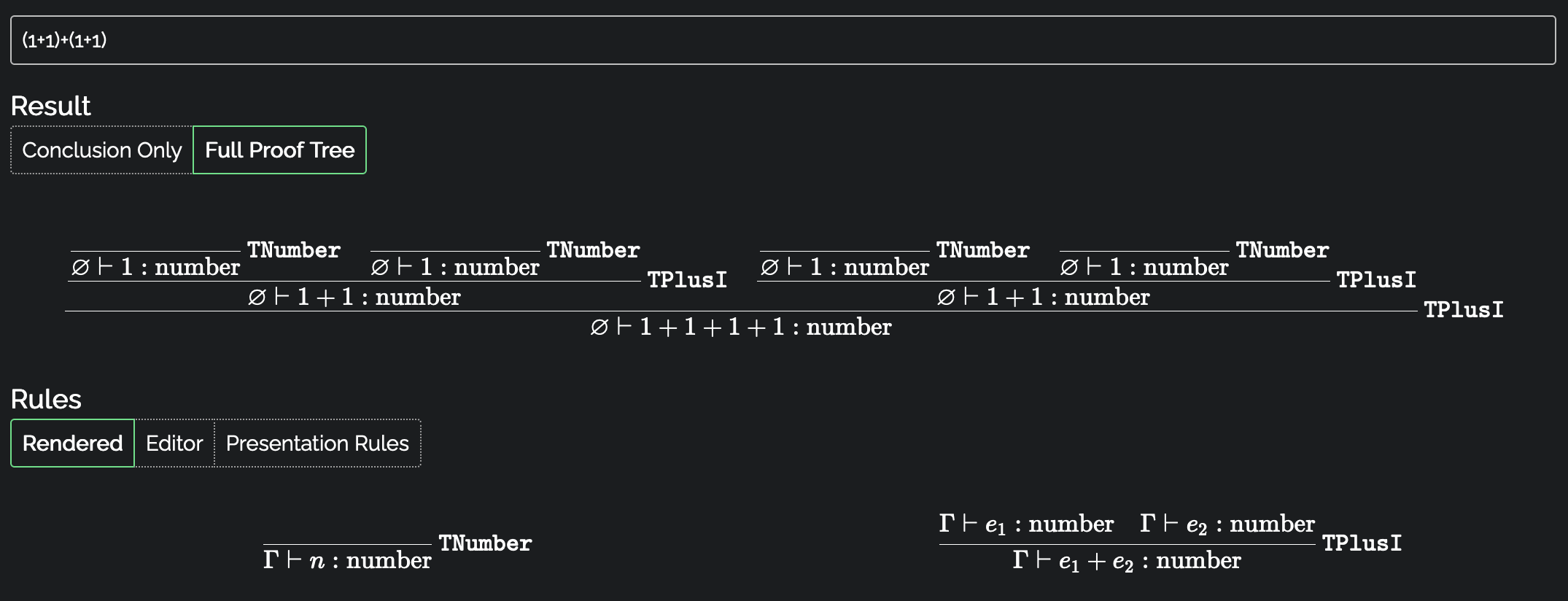
Verifying the (1+1)+(1+1) expression using the good rule
On the other hand, since the sum of two xs and two ys doesn’t work with my old rules, maybe
i wouldn’t get a valid type at all:

Verifying (unsuccessfully) the (x+x)+(y+y) expression using the old rule
More generally, I want to be able to write down some inference rules, and apply them to some programs. This way, I can see what works and what doesn’t, and when it works, which rules were used for what purposes. I also want to be able to try tweaking, removing, or adding inference rules, to see what breaks.
This brings me to the project that I’m trying to show off in this post: Bergamot!
Introducing Bergamot
A certain class of programming languages lends itself particularly well to writing inference rules and applying them to programs: logic programming. The most famous example of a logic programming language is Prolog. In logic programming languages like Prolog, we can write rules describing when certain statements should hold. The simplest rule I could write is a fact. Perhaps I’d like to say that the number 42 is a “good” number:
good(42).
Perhaps I’d then like to say that adding two good numbers together creates another good number.
good(N) :- good(A), good(B), N is A+B.
The above can be read as:
the number
Nis good if the numbersAandBare good, andNis the sum ofAandB.
I can then ask Prolog to give me some good numbers:
?- good(X)
Prompting Prolog a few times, I get:
X = 42
X = 84
X = 126
X = 168
It’s not a huge leap from this to programming language type rules. Perhaps instead
of something being “good”, we can say that it has type string. Of course, adding
two strings together, as we’ve established, creates another string. In Prolog:
/* A string literal like "hello" has type string */
type(_, strlit(_), string).
/* Adding two string expressions has type string */
type(Env, plus(X, Y), string) :- type(Env, X, string), type(Env, Y, string).
That’s almost identical to our inference rules above, except that it’s written using code instead of mathematical notation! If we could just take these Prolog rules and display them as inference rules, we’d be able to “have our cake” (draw pretty inference rules like in the papers) and “eat it too” (run our rules on the computer against various programs).
This is where it gets a teensy bit hairy. It’s not that easy to embed a Prolog engine into the browser; alternatives that I’ve surveyed are either poorly documented, hard to extend, or both. Furthermore, for studying what each rule was used for, it’s nice to be able to see a proof tree: a tree made up from the rules that we used to arrive at a particular answer. Prolog engines are excellent at applying rules and finding answers, but they don’t usually provide a way to get all the rules that were used, making it harder to get proof trees.
Thus, Bergamot is a new, tiny programming language that I threw together in a couple of days. It comes as JavaScript-based widget, and can be embedded into web pages like this one to provide an interactive way to write and explore proof trees. Here’s a screenshot of what all of that looks like:

A screenshot of a Bergamot widget with some type rules
The components of Bergamot are:
- The programming language, as stated above. This language is a very simple, unification-based logic programming language.
- A rule rendering system, which takes Prolog-like rules written in Bergamot and converts them into pretty LaTeX inference rules.
- An Elm-based widget that you can embed into your web page, which accepts Bergamot rule and an input expression, and applies the rules to produce a result (or a whole proof tree!).
Much like in Prolog, we can write Bergamot rules that describe when certain things are true. Unlike Prolog, Bergamot requires each rule to have a name. This is common practice in programming languages literature (when we talk about rules in papers, we like to be able to refer to them by name). Below are some sample Bergamot rules, corresponding to the first few inference rules in the above screenshot.
TNumber @ type(?Gamma, intlit(?n), number) <-;
TString @ type(?Gamma, strlit(?s), string) <-;
TVar @ type(?Gamma, var(?x), ?tau) <- inenv(?x, ?tau, ?Gamma);
TPlusI @ type(?Gamma, plus(?e_1, ?e_2), number) <-
type(?Gamma, ?e_1, number), type(?Gamma, ?e_2, number);
TPlusS @ type(?Gamma, plus(?e_1, ?e_2), string) <-
type(?Gamma, ?e_1, string), type(?Gamma, ?e_2, string);
Unlike Prolog, where “variables” are anything that starts with a capital letter,
in Bergamot, variables are things that start with the special ? symbol. Also,
Prolog’s :- has been replaced with an arrow symbol <-, for reverse implication.
These are both purely syntactic differences.
Demo
If you want to play around with it, here’s an embedded Bergamot widget with
[note:
Actually, one of the rules is incorrect to my knowledge. Can you spot it?
Hint: is \x : number. \x: string. x+1 well-typed? What does
Bergamot report? Can you see why?
]
It has two modes:
-
Language Term: accepts a rather simple programming language
to typecheck. Try
1+1,fst((1,2)), or maybe(\x : number. x) 42. -
Query: it accepts Bergamot expressions to query, similarly to Prolog; try
type(empty, ?e, tpair(number, string))to search for expressions that have the type “a pair of a number and a string”.
Rendering Bergamot with Bergamot
There’s something to be said about the conversion between Bergamot’s rules, encoded as plain text, and pretty LaTeX-based inference rules that the users see. Crucially, we don’t want to hardcode how any particular Bergamot expression is rendered. For one, this is a losing battle: we can’t possibly keep up with all the notation that people use in PL literature, and even if we focused ourselves on only “beginner” notation, there wouldn’t be one way to do it! Different PL papers and texts use slightly different variations of notation. For instance, I render my pairs as , but the very first screenshot in this post demonstrates a PL paper that writes pairs as . Neither way (as far as I know!) is right or wrong. But if we hardcode one, we lose the ability to draw the other.
More broadly, one aspect about writing PL rules is that we control the notation. We are free to define shorthands, symbols, and anything else that would make reading our rules easier for others. As an example, a paper from POPL22 about programming language semantics with garbage collection used a literal trash symbol in their rules:
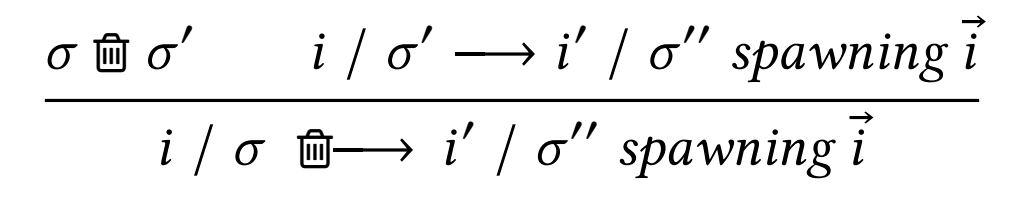
A rule that uses a trashcan icon as notation, from A separation logic for heap space under garbage collection by Jean-Marie Madiot and François Pottier
Thus, what I want to do is encourage the (responsible) introduction of new notation. This can only be done if Bergamot itself supports custom notation.
When thinking about how I’d like to implement this custom notation, I was imagining some sort of templated rule engine, that would define how each term in a Bergamot program can be converted to its LaTeX variant. But then I realized: Bergamot is already a rule engine! Instead of inventing yet another language or format for defining LaTeX pretty printing, I could just use Bergamot. This turned out to work quite nicely – the “Presentation Rules” tab in the demo above should open a text editor with Bergamot rules that handle the conversion of Bergamot notation into LaTex. Here are some example rules:
LatexPlus @ latex(plus(?e_1, ?e_2), ?l) <- latex(?e_1, ?l_1), latex(?e_2, ?l_2), join([?l_1, " + ", ?l_2], ?l);
LatexPair @ latex(pair(?e_1, ?e_2), ?l) <- latex(?e_1, ?l_1), latex(?e_2, ?l_2), join(["(", ?l_1, ", ", ?l_2, ")"], ?l);
If we change the LatexPair to the following, we can make all pairs render
using angle brackets:
LatexPair @ latex(pair(?e_1, ?e_2), ?l) <- latex(?e_1, ?l_1), latex(?e_2, ?l_2), join(["\\langle", ?l_1, ", ", ?l_2, "\\rangle"], ?l);

The LaTeX output when angle brackets are used in the rule instead of parentheses.
You can write rules about arbitrary Bergamot terms for rendering; thus, you can invent completely new notation for absolutely anything.
Next Steps
I hope to use Bergamot to write a series of articles about type systems. By providing an interactive widget, I hope to make it possible for users to do exercises: writing variations of inference rules, or even tweaking the notation, and checking them against sets of programs to make sure that they work. Of course, I also hope that Bergamot can be used to explore why an existing set of inference rules (such as Hindley-Milner) works. Stay tuned for those!