Now that our language’s type system is more fleshed out and pleasant to use, it’s time to shift our focus to the ergonomics of the language itself. I’ve been mentioning let/in and lambda expressions for a while now. The former will let us create names for expressions that are limited to a certain scope (without having to create global variable bindings), while the latter will allow us to create functions without giving them any name at all.
Let’s take a look at let/in expressions first, to make sure we’re all on the same page about what it is we’re trying to implement. Let’s start with some rather basic examples, and then move on to more complex ones. A very basic use of a let/in expression is, in Haskell:
let x = 5 in x + x
In the above example, we bind the variable x to the value 5, and then refer to x twice in the expression after the in. The whole snippet is one expression, evaluating to what the in part evaluates to. Additionally, the variable x does not escape the expression -
[note:
Unless, of course, you bind it elsewhere; naturally, using x here does not forbid you from re-using the variable.
]
Now, consider a slightly more complicated example:
let sum xs = foldl (+) 0 xs in sum [1,2,3]
Here, we’re defining a function sum,
[note:
Those who favor the
point-free
programming style may be slightly twitching right now, the words eta reduction swirling in their mind. What do you know, fold-based sum is even one of the examples on the Wikipedia page! I assure you, I left the code as you see it deliberately, to demonstrate a principle.
]
the list to be summed. We will want this to be valid in our language, as well. We will soon see how this particular feature is related to lambda functions, and why I’m covering these two features in the same post.
Let’s step up the difficulty a bit more, with an example that,
[note:
The part that doesn't translate well is the whole deal with patterns in function arguments, as well as the notion of having more than one equation for a single function, as is the case with safeTail.
It's not that these things are impossible to translate; it's just that translating them may be worthy of a post in and of itself, and would only serve to bloat and complicate this part. What can be implemented with pattern arguments can just as well be implemented using regular case expressions; I dare say most "big" functional languages actually just convert from the former to the latter as part of the compillation process.
]
illustrates another important principle:
|
|
The principle here is that definitions in let/in can be recursive and polymorphic. Remember the note in
part 10 about
let-polymorphism? This is it: we’re allowing polymorphic variable bindings, but only when they’re bound in a let/in expression (or at the top level).
The principles demonstrated by the last two snippets mean that compiling let/in expressions, at least with the power we want to give them, will require the same kind of dependency analysis we had to go through when we implemented polymorphically typed functions. That is, we will need to analyze which functions calls which other functions, and typecheck the callees before the callers. We will continue to represent callee-caller relationships using a dependency graph, in which nodes represent functions, and an edge from one function node to another means that the former function calls the latter. Below is an image of one such graph:
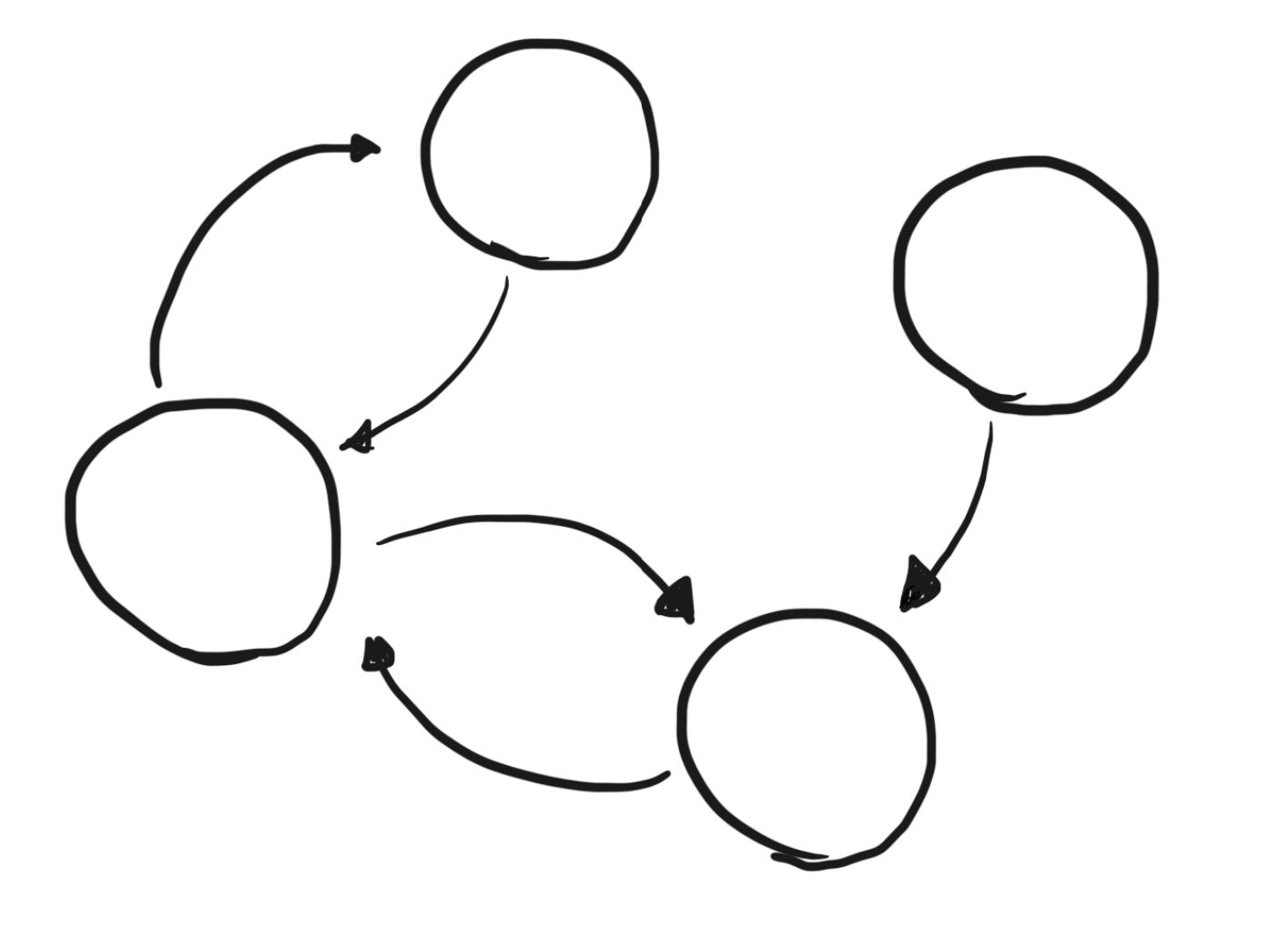
Example dependency graph without let/in expressions.
Since we want to typecheck callees first, we effectively want to traverse the graph in reverse topological order. However, there’s a slight issue: a topological order is only defined for acyclic graphs, and it is very possible for functions in our language to mutually call each other. To deal with this, we have to find groups of mutually recursive functions, and and treat them as a single unit, thereby eliminating cycles. In the above graph, there are two groups, as follows:
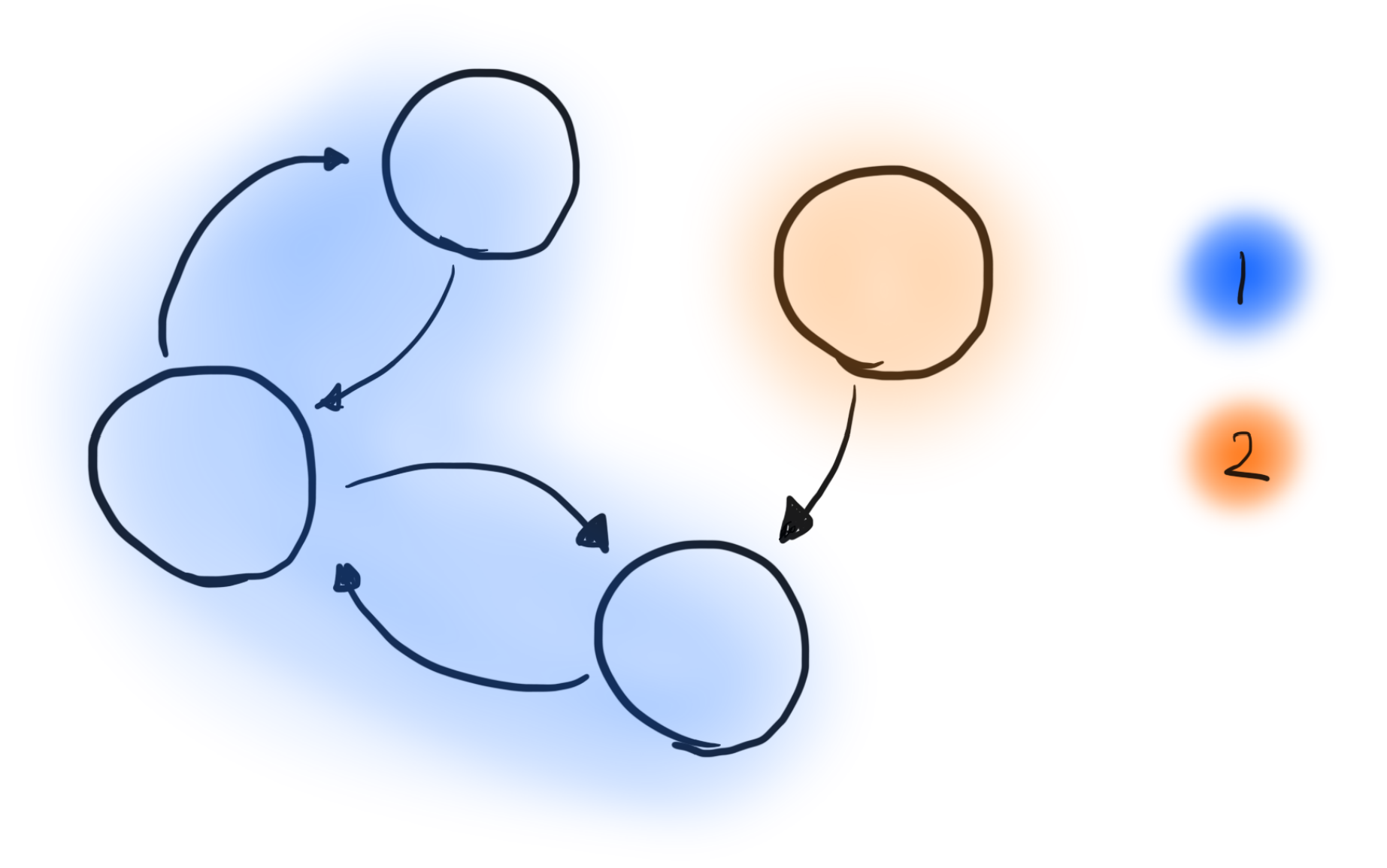
Previous depndency graph with mutually recursive groups highlighted.
As seen in the second image, according to the reverse topological order of the given graph, we will typecheck the blue group containing three functions first, since the sole function in the orange group calls one of the blue functions.
Things are more complicated now that let/in expressions are able to introduce their own, polymorphic and recursive declarations. However, there is a single invariant we can establish: function definitions can only depend on functions defined at the same time as them. That is, for our purposes, functions declared in the global scope can only depend on other functions declared in the global scope, and functions declared in a let/in expression can only depend on other functions declared in that same expression. That’s not to say that a function declared in a let/in block inside some function f can’t call another globally declared function g - rather, we allow this, but treat the situation as though f depends on g. In contrast, it’s not at all possible for a global function to depend on a local function, because bindings created in a let/in expression do not escape the expression itself. This invariant tells us that in the presence of nested function definitions, the situation looks like this:
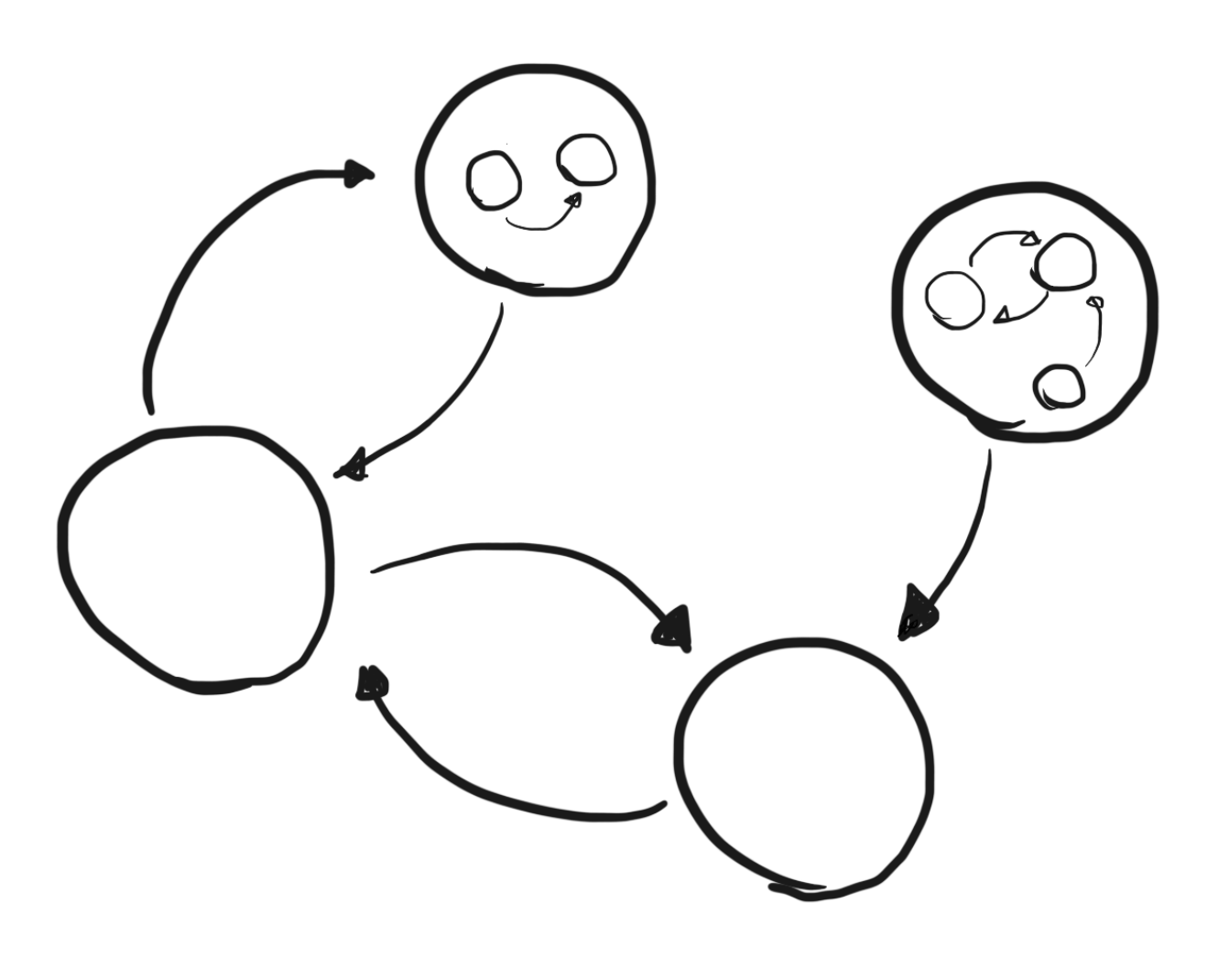
Previous depndency graph augmented with let/in subgraphs.
In the above image, some of the original nodes in our graph now contain other, smaller graphs. Those subgraphs are the graphs created by function declarations in let/in expressions. Just like our top-level nodes, the nodes of these smaller graphs can depend on other nodes, and even form cycles. Within each subgraph, we will have to perform the same kind of cycle detection, resulting in something like this:
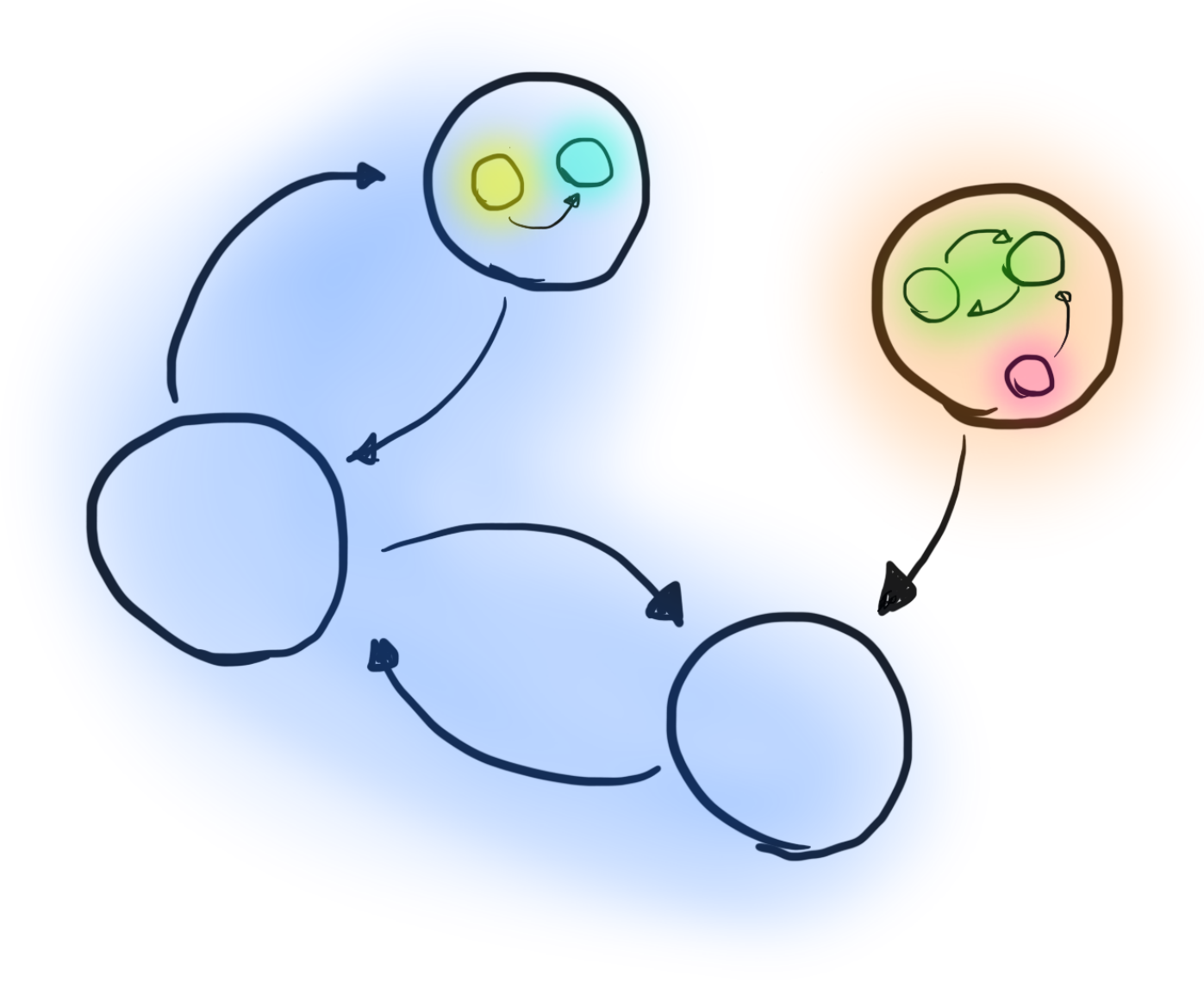
Augmented dependency graph with mutually recursive groups highlighted.
When typechecking a function, we must be ready to perform dependency analysis at any point. What’s more is that the free variable analysis we used to perform must now be extended to differentiate between free variables that refer to “nearby” definitions (i.e. within the same let/in expression), and “far away” definitions (i.e. outside of the let/in expression). And speaking of free variables…
What do we do about variables that are captured by a local definition? Consider the following snippet:
|
|
In the code above, the variable n, bound on line 1, is used by addSingle on line 3. When a function refers to variables bound outside of itself (as addSingle does), it is said to be capturing these variables, and the function is called a closure. Why does this matter? On the machine level, functions are represented as sequences of instructions, and there’s a finite number of them (as there is finite space on the machine). But there is an infinite number of addSingle functions! When we write addToAll 5 [1,2,3], addSingle becomes 5+x. When, on the other hand, we write addToAll 6 [1,2,3], addSingle becomes 6+x. There are certain ways to work around this - we could, for instance, dynamically create machine code in memory, and then execute it (this is called just-in-time compilation). This would end up with a collections of runtime-defined functions that can be represented as follows:
|
|
But now, we end up creating several functions with almost identical bodies, with the exception of the free variables themselves. Wouldn’t it be better to perform the well-known strategy of reducing code duplication by factoring out parameters, and leaving only one instance of the repeated code? We would end up with:
|
|
Observe that we no longer have the “infinite” number of functions - the infinitude of possible behaviors is created via currying. Also note that addSingle
[note:
Wait a moment, didn't we just talk about nested polymorphic definitions, and how they change our typechecking model? If we transform our program into a bunch of global definitions, we don't need to make adjustments to our typechecking.
This is true, but why should we perform transformations on a malformed program? Typechecking before pulling functions to the global scope will help us save the work, and breaking down one dependency-searching problem (which is thanks to Warshall's) into smaller, independent problems may even lead to better performance. Furthermore, typechecking before program transformations will help us come up with more helpful error messages.
]
and can be transformed into a sequence of instructions just like any other global function. It has been pulled from its where (which, by the way, is pretty much equivalent to a let/in) to the top level.
Now, see how addSingle became (addSingle n)? If we chose to rewrite the
program this way, we’d have to find-and-replace every instance of addSingle
in the function body, which would be tedious and require us to keep
track of shadowed variables and the like. Also, what if we used a local
definition twice in the original piece of code? How about something like this:
|
|
Applying the strategy we saw above, we get:
|
|
This is valid, except that in our evaluation model, the two instances
of (square x) will be built independently of one another, and thus,
will not be shared. This, in turn, will mean that square will be called
twice, which is not what we would expect from looking at the original program.
This isn’t good. Instead, why don’t we keep the where, but modify it
as follows:
|
|
This time, assuming we can properly implement where, the call to
square' x should only occur once. Though I’ve been using where,
which leads to less clutter in Haskell code, the exact same approach applies
to let/in, and that’s what we’ll be using in our language.
This technique of replacing captured variables with arguments, and pulling closures into the global scope to aid compilation, is called Lambda Lifting. Its name is no coincidence - lambda functions need to undergo the same kind of transformation as our nested definitions (unlike nested definitions, though, lambda functions need to be named). This is why they are included in this post together with let/in!
What are lambda functions, by the way? A lambda function is just a function expression that doesn’t have a name. For example, if we had Haskell code like this:
double x = x + x
doubleList xs = map double xs
We could rewrite it using a lambda function as follows:
doubleList xs = map (\x -> x + x) xs
As you can see, a lambda is an expression in the form \x -> y where x can
be any variable and y can be any expression (including another lambda).
This represents a function that, when applied to a value x, will perform
the computation given by y. Lambdas are useful when creating single-use
functions that we don’t want to make globally available.
Lifting lambda functions will effectively rewrite our program in the
opposite direction to the one shown, replacing the lambda with a reference
to a global declaration which will hold the function’s body. Just like
with let/in, we will represent captured variables using arguments
and partial appliciation. For instance, when starting with:
addToAll n xs = map (\x -> n + x) xs
We would output the following:
addToAll n xs = map (lambda n) xs
lambda n x = n + x
Implementation
Now that we understand what we have to do, it’s time to jump straight into
doing it. First, we need to refactor our current code to allow for the changes
we’re going to make; then, we will use the new tools we defined to implement let/in expressions and lambda functions.
Infrastructure Changes
When finding captured variables, the notion of free variables once again becomes important. Recall that a free variable in an expression is a variable that is defined outside of that expression. Consider, for example, the expression:
let x = 5 in x + y
In this expression, x is not a free variable, since it’s defined
in the let/in expression. On the other hand, y is a free variable,
since it’s not defined locally.
The algorithm that we used for computing free variables was rather biased.
Previously, we only cared about the difference between a local variable
(defined somewhere in a function’s body, or referring to one of the function’s
parameters) and a global variable (referring to a global function).
This shows in our code for find_free. Consider, for example, this snippet:
|
|
We created bindings in our type environment whenever we saw a new variable being introduced, which led us to only count variables that we did not bind anywhere as ‘free’. This approach is no longer sufficient. Consider, for example, the following Haskell code:
|
|
We can see that the variable x is introduced on line 1.
Thus, our current algorithm will happily store x in an environment,
and not count it as free. But clearly, the definition of y on line 3
captures x! If we were to lift y into global scope, we would need
to pass x to it as an argument. To fix this, we have to separate the creation
and assignment of type environments from free variable detection. Why
don’t we start with ast and its descendants? Our signatures become:
void ast::find_free(std::set<std::string>& into);
type_ptr ast::typecheck(type_mgr& mgr, type_env_ptr& env);
For the most part, the code remains unchanged. We avoid
using env (and this->env), and default to marking
any variable as a free variable:
|
|
Since we no longer use the environment, we resort to an
alternative method of removing bound variables. Here’s
ast_case::find_free:
|
|
For each branch, we find the free variables. However, we
want to avoid marking variables that were introduced through
pattern matching as free (they are not). Thus, we use pattern::find_variables
to see which of the variables were bound by that pattern,
and remove them from the list of free variables. We
can then safely add the list of free variables in the pattern to the overall
list of free variables. Other ast descendants experience largely
cosmetic changes (such as the removal of the env parameter).
Of course, we must implement find_variables for each of our pattern
subclasses. Here’s what I got for pattern_var:
|
|
And here’s an equally terse implementation for pattern_constr:
|
|
We also want to update definition_defn with this change. Our signatures
become:
void definition_defn::find_free();
void definition_defn::insert_types(type_mgr& mgr, type_env_ptr& env, visibility v);
We’ll get to the visiblity parameter later. The implementations
are fairly simple. Just like ast_case, we want to erase each function’s
parameters from its list of free variables:
|
|
Since find_free no longer creates any type bindings or environments,
this functionality is shouldered by insert_types:
|
|
Now that free variables are properly computed, we are able to move on to bigger and better things.
Nested Definitions
At present, our code for typechecking the whole program is located in
main.cpp:
|
|
This piece of code goes on. We now want this to be more general. Soon, let/in
expressions with bring with them definitions that are inside other definitions,
which will not be reachable at the top level. The fundamental topological
sorting algorithm, though, will remain the same. We can abstract a series
of definitions that need to be ordered and then typechecked into a new struct,
definition_group:
|
|
This will be exactly like a list of defn/data definitions we have at the
top level, except now, it can also occur in other places, like let/in
expressions. Once again, ignore for the moment the visibility field.
The way we defined function ordering requires some extra work from
definition_group. Recall that conceptually, functions can only depend
on other functions defined in the same let/in expression, or, more generally,
in the same definition_group. This means that we now classify free variables
in definitions into two categories: free variables that refer to “nearby”
definitions (i.e. definitions in the same group) and free variables that refer
to “far away” definitions. The “nearby” variables will be used to do
topological ordering, while the “far away” variables can be passed along
further up, perhaps into an enclosing let/in expression (for which “nearby”
variables aren’t actually free, since they are bound in the let). We
implement this partitioning of variables in definition_group::find_free:
|
|
Notice that we have added a new nearby_variables field to definition_defn.
This is used on line 101, and will be once again used in definition_group::typecheck. Speaking of typecheck, let’s look at its definition:
|
|
This function is a little long, but conceptually, each for loop
contains a step of the process:
- The first loop declares all data types, so that constructors can be verified to properly reference them.
- The second loop creates all the data type constructors.
- The third loop adds edges to our dependency graph.
- The fourth loop performs typechecking on the now-ordered groups of mutually
recursive functions.
- The first inner loop inserts the types of all the functions into the environment.
- The second inner loop actually performs typechecking.
- The third inner loop makes as many things polymorphic as possible.
We can now adjust our parser.y to use a definition_group instead of
two global vectors. First, we declare a global definition_group:
|
|
Then, we adjust definitions to create definition_groups:
|
|
We can now adjust main.cpp to use the global definition_group. Among
other changes (such as removing extern references to vectors, and updating
function signatures) we also update the typecheck_program function:
|
|
Now, our code is ready for typechecking nested definitions, but not for compiling them. The main thing that we still have to address is the addition of new definitions to the global scope. Let’s take a look at that next.
Global Definitions
We want every function (and even non-function definitions that capture surrounding
variables), regardless of whether or not it was declared in the global scope,
to be processed and converted to LLVM code. The LLVM code conversion takes
several steps. First, the function’s AST is translated into G-machine
instructions, which we covered in part 5,
by a process we covered in part 6.
Then, an LLVM function is created for every function, and registered globally.
Finally, the G-machine instructions are converted into LLVM IR, which is
inserted into the previously created functions. These things
can’t be done in a single pass: at the very least, we can’t start translating
G-machine instructions into LLVM IR until functions are globally declared,
because we would otherwise have no means of referencing other functions. It
makes sense to me, then, to pull out all the ‘global’ definitions into
a single top-level list (perhaps somewhere in main.cpp).
Let’s start implementing this with a new global_scope struct. This
struct will contain all of the global function and constructor definitions:
|
|
This struct will allow us to keep track of all the global definitions,
emitting them as we go, and then coming back to them as necessary.
There are also signs of another piece of functionality: occurence_count
and mangle_name. These two will be used to handle duplicate names.
We cannot have two global functions named the same thing, but we can
easily imagine a situation in which two separate let/in expressions define
a variable like x, which then needs to be lifted to the global scope. We
resolve such conflicts by slightly changing - “mangling” - the name of
one of the resulting global definitions. We allow the first global definition
to be named the same as it was originally (in our example, this would be x).
However, if we detect that a global definition x already exists (we
track this using occurence_count), we rename it to x_1. Subsequent
global definitions will end up being named x_2, x_3, and so on.
Alright, let’s take a look at global_function and global_constructor.
Here’s the former:
|
|
There’s nothing really surprising here: all of the fields
are reminiscent of definition_defn, though some type-related variables
are missing. We also include the three compilation-related methods,
compile, declare_llvm, and generate_llvm, which were previously in definition_defn. Let’s look at global_constructor now:
|
|
This maps pretty closely to a single definition_data::constructor.
There’s a difference here that is not clear at a glance, though. Whereas
the name in a definition_defn or definition_data refers to the
name as given by the user in the code, the name of a global_function
or global_constructor has gone through mangling, and thus, should be
unique.
Let’s now look at the implementation of these structs’ methods. The methods
add_function and add_constructor are pretty straightforward. Here’s
the former:
|
|
And here’s the latter:
|
|
In both of these functions, we return a reference to the new global
definition we created. This helps us access the mangled name field,
and, in the case of global_function, inspect the ast_ptr that represents
its body.
Next, we have global_scope::compile and global_scope::generate_llvm,
which encapsulate these operations on all global definitions. Their
implementations are very straightforward, and are similar to the
gen_llvm function we used to have in our main.cpp:
|
|
Finally, we have mangle, which takes care of potentially duplicate
variable names:
|
|
Let’s move on to the global definition structs.
The compile, declare_llvm, and generate_llvm methods for
global_function are pretty much the same as those that we used to have
in definition_defn:
|
|
The same is true for global_constructor and its method generate_llvm:
|
|
Recall that in this case, we need not have two methods for declaring and generating LLVM, since constructors don’t reference other constructors, and are always generated before any function definitions.
Visibility
Should we really be turning all free variables in a function definition into arguments? Consider the following piece of Haskell code:
|
|
In the definition of something, mul and add occur free.
A very naive lifting algorithm might be tempted to rewrite such a program
as follows:
|
|
But that’s absurd! Not only are add and mul available globally,
but such a rewrite generates another definition with free variables,
which means we didn’t really improve our program in any way. From this
example, we can see that we don’t want to be turning reference to global
variables into function parameters. But how can we tell if a variable
we’re trying to operate on is global or not? I propose a flag in our
type_env, which we’ll augment to be used as a symbol table. To do
this, we update the implementation of type_env to map variables to
values of a struct variable_data:
|
|
The visibility enum is defined as follows:
|
|
As you can see from the above snippet, we also added a mangled_name field
to the new variable_data struct. We will be using this field shortly. We
also add a few methods to our type_env, and end up with the following:
|
|
We will come back to find_free and find_free_except, as well as
set_mangled_name and get_mangled_name. For now, we just adjust bind to
take a visibility parameter that defaults to local, and implement
is_global:
|
|
Remember the visibility::global in parser.y? This is where that comes in.
Specifically, we recall that definition_defn::insert_types is responsible
for placing function types into the environment, making them accessible
during typechecking later. At this time, we already need to know whether
or not the definitions are global or local (so that we can create the binding).
Thus, we add visibility as a parameter to insert_types:
|
|
Since we are now moving from manually wrangling definitions towards using
definition_group, we make it so that the group itself provides this
argument. To do this, we add the visibility field from before to it,
and set it in the parser. One more thing: since constructors never
capture variables, we can always move them straight to the global
scope, and thus, we’ll always mark them with visibility::global.
Managing Mangled Names
Just mangling names is not enough. Consider the following program:
|
|
[note:
We are actually not quite doing something like the following snippet.
The reason for this is that we don't mangle the names for types. I pointed
out this potential issue in a sidenote in the previous post. Since the size
of this post is already balooning, I will not deal with this issue here.
Even at the end of this post, our compiler will not be able to distinguish
between the two Packed types. We will hopefully get to it later.
]
and their constructors into the global
scope gives us something like:
data Packed a = { Pack a }
data Packed_1 a = { Pack_1 a }
defn packOne x = { Pack x }
defn packTwo x = { Pack_1 x }
Notice that we had to rename one of the calls to Pack to be a call to
be Pack_1. To actually change our AST to reference Pack_1, we’d have
to traverse the whole tree, and make sure to keep track of definitions
that could shadow Pack further down. This is cumbersome. Instead, we
can mark a variable as referring to a mangled version of itself, and
access this information when needed. To do this, we add the mangled_name
field to the variable_data struct as we’ve seen above, and implement
the set_mangled_name and get_mangled_name methods. The former:
|
|
And the latter:
|
|
We don’t allow set_mangled_name to affect variables that are declared
above the receiving type_env, and use the empty string as a ’none’ value.
Now, when lifting data type constructors, we’ll be able to use
set_mangled_name to make sure constructor calls are made correctly. We
will also be able to use this in other cases, like the translation
of local function definitions.
New AST Nodes
Finally, it’s time for us to add new AST nodes to our language.
Specifically, these nodes are ast_let (for let/in expressions)
and ast_lambda for lambda functions. We declare them as follows:
|
|
In ast_let, the definitions field corresponds to the original definitions
given by the user in the program, and the in field corresponds to the
expression which uses these definitions. In the process of lifting, though,
we eventually transfer each of the definitions to the global scope, replacing
their right hand sides with partial applications. After this transformation,
all the data type definitions are effectively gone, and all the function
definitions are converted into the simple form x = f a1 ... an. We hold
these post-transformation equations in the translated_definitions field,
and it’s them that we compile in this node’s compile method.
In ast_lambda, we allow multiple parameters (like Haskell’s \x y -> x + y).
We store these parameters in the params field, and we store the lambda’s
expression in the body field. Just like definition_defn,
the ast_lambda node maintains a separate environment in which its children
have been bound, and a list of variables that occur freely in its body. The
former is used for typechecking, while the latter is used for lifting.
Finally, the translated field holds the lambda function’s form
after its body has been transformed into a global function. Similarly to
ast_let, this node will be in the form f a1 ... an.
The
observant reader will have noticed that we have a new method: translate.
This is a new method for all ast descendants, and will implement the
steps of moving definitions to the global scope and transforming the
program. Before we get to it, though, let’s look at the other relevant
pieces of code for ast_let and ast_lambda. First, their grammar
rules in parser.y:
|
|
This is pretty similar to the rest of the grammar, so I will give this no
further explanation. Next, their find_free and typecheck code.
We can start with ast_let:
|
|
As you can see, ast_let::find_free works in a similar manner to ast_case::find_free.
It finds the free variables in the in node as well as in each of the definitions
(taking advantage of the fact that definition_group::find_free populates the
given set with “far away” free variables). It then filters out any variables bound in
the let from the set of free variables in in, and returns the result.
Typechecking in ast_let relies on definition_group::typecheck, which holds
all of the required functionality for checking the new definitions.
Once the definitions are typechecked, we use their type information to
typecheck the in part of the expression (passing definitions.env to the
call to typecheck to make the new definitions visible).
Next, we look at ast_lambda:
|
|
Again, ast_lambda::find_free works similarly to definition_defn, stripping
the variables expected by the function from the body’s list of free variables.
Also like definition_defn, this new node remembers the free variables in
its body, which we will later use for lifting.
Typechecking in this node also proceeds similarly to definition_defn. We create
new type variables for each parameter and for the return value, and build up
a function type called full_type. We then typecheck the body using the
new environment (which now includes the variables), and return the function type we came up with.
Translation
Recalling the transformations we described earlier, we can observe two major steps to what we have to do:
- Move the body of the original definition into its own global definition, adding all the captured variables as arguments.
- Replace the right hand side of the
let/inexpression with an application of the global definition to the variables it requires.
We will implement these in a new translate method, with the following
signature:
void ast::translate(global_scope& scope);
The scope parameter and its add_function and add_constructor methods will
be used to add definitions to the global scope. Each AST node will also
use this method to implement the second step. Currently, only
ast_let and ast_lambda will need to modify themselves - all other
nodes will simply recursively call this method on their children. Let’s jump
straight into implementing this method for ast_let:
|
|
Since data type definitions don’t really depend on anything else, we process
them first. This amounts to simply calling the definition_data::into_globals
method, which itself simply calls global_scope::add_constructor:
|
|
Note how into_globals updates the mangled name of its constructor
via set_mangled_name. This will help us decide which global
function to call during code generation. More on that later.
Starting with line 295, we start processing the function definitions
in the let/in expression. We remember how many arguments were
explicitly added to the function definition, and then call the
definition’s into_global method. This method is implemented
as follows:
|
|
First, this method collects all the non-global free variables in
its body, which will need to be passed to the global definition
as arguments. It then combines this list with the arguments
the user explicitly added to it, recursively translates
its body, and creates a new global definition using add_function.
We return to ast_let::translate at line 299. Here,
we determine how many variables ended up being captured, by
subtracting the number of explicit parameters from the total
number of parameters the new global definition has. This number,
combined with the fact that we added all the ‘implict’ arguments
to the function to the beginning of the list, will let us
iterate over all implict arguments, creating a chain of partial
function applications.
But how do we build the application? We could use the mangled name
of the function, but this seems inelegant, especially since we
alreaady keep track of mangling information in type_env. Instead,
we create a new, local environment, in which we place an updated
binding for the function, marking it global, and setting
its mangled name to the one generated by global_sope. This work is done
on lines 301-303. We create a reference to the global function
using the new environment on lines 305 and 306, and apply it to
all the implict arguments on lines 307-313. Finally, we
add the new ‘basic’ equation into translated_definitions.
Let’s take a look at translating ast_lambda next:
|
|
Once again, on lines 369-375 we find all the arguments to the
global definition. On lines 377-382 we create a new global
function and a mangled environment, and start creating the
chain of function applications. On lines 384-390, we actually
create the arguments and apply the function to them. Finally,
on line 391, we store this new chain of applications in the
translated field.
Compilation
There’s still another piece of the puzzle missing, and
that’s how we’re going to compile let/in expressions into
G-machine instructions. We have allowed these expressions
to be recursive, and maybe even mutually recursive. This
worked fine with global definitions; instead of specifying
where on the stack we can find the reference to a global
function, we just created a new global node, and called
it good. Things are different now, though, because the definitions
we’re referencing aren’t just global functions; they are partial
applications of a global function. And to reference themselves,
or their neighbors, they have to have a handle on their own nodes. We do this
using an instruction that we foreshadowed in part 5, but didn’t use
until just now: Alloc.
Alloc creates placeholder nodes on the stack. These nodes are indirections, the same kind that we use for lazy evaluation and sharing elsewhere. We create an indirection node for every definition that we then build; when an expression needs access to a definition, we give it the indirection node. After building the partial application graph for an expression, we use Update, making the corresponding indirection point to this new graph. This way, the ‘handle’ to a definition is always accessible, and once the definition’s expression is built, the handle correctly points to it. Here’s the implementation:
|
|
First, we create the Alloc instruction. Then, we update
our environment to map each definition name to a location
within the newly allocated batch of nodes. Since we iterate
the definitions in order, ‘pushing’ them into our environment,
we end up with the convention of having the later definitions
closer to the top of the G-machine stack. Thus, when we
iterate the definitions again, this time to compile their
bodies, we have to do so starting with the highest offset,
and working our way down to Update-ing the top of the stack.
Once the definitions have been compiled, we proceed to compiling
the in part of the expression as normal, using our updated
environment. Finally, we use Slide to get rid of the definition
graphs, cleaning up the stack.
Compiling the ast_lambda is far more straightforward. We just
compile the resulting partial application as we normally would have:
|
|
One more thing. Let’s adopt the convention of storing mangled
names into the compilation environment. This way, rather than looking up
mangled names only for global functions, which would be a ‘gotcha’
for anyone working on the compiler, we will always use the mangled
names during compilation. To make this change, we make sure that
ast_case also uses mangled_name:
|
|
We also update the logic for ast_lid::compile to use the mangled
name information:
|
|
Fixing Type Generalization
This is a rather serious bug that made its way into the codebase
since part 10. Recall that we can only generalize type variables
that are free in the environment. Thus far, we haven’t done that,
and we really should: I ran into incorrectly inferred types
in my first test of the let/in language feature.
We need to make our code capable of finding free variables in the
type environment. This requires the type_mgr, which associates
with type variables the real types they represent, if any. We
thus create methods with signatures as follows:
void type_env::find_free(const type_mgr& mgr, std::set<std::string>& into) const;
void type_env::find_free_except(const type_mgr& mgr, const std::string& avoid,
std::set<std::string>& into) const;
Why find_free_except? When generalizing a variable whose type was already
stored in the environment, all the type variables we could generalize would
not be ‘free’. If they only occur in the type we’re generalizing, though,
we shouldn’t let that stop us! More generally, if we see type variables that
are only found in the same mutually recursive group as the binding we’re
generalizing, we are free to generalize them too. Thus, we pass in
a reference to a group, and check if a variable is a member of that group
before searching it for free type variables. The implementations of the two
methods are straightforward:
|
|
Note that find_free_except calls find_free in its recursive call. This
is not a bug: we do want to include free type variables from bindings
that have the same name as the variable we’re generalizing, but aren’t found
in the same scope. As far as we’re concerned, they’re different variables!
The two methods use another find_free method which we add to type_mgr:
|
|
This one is a bit of a hack. Typically, while running find_free, a
type_mgr will resolve any type variables. However, variables from the
forall quantifier of a type scheme should not be resolved, since they
are explicitly generic. To prevent the type manager from erroneously resolving
such type variables, we create a new type manager that does not have
these variables bound to anything, and thus marks them as free. We then
filter these variables out of the final list of free variables.
Finally, generalize makes sure not to use variables that it finds free:
|
|
Putting It All Together
All that’s left is to tie the parts we’ve created into one coherent whole
in main.cpp. First of all, since we moved all of the LLVM-related
code into global_scope, we can safely replace that functionality
in main.cpp with a method call:
|
|
On the other hand, we need top-level logic to handle definition_groups.
This is pretty straightforward, and the main trick is to remember to
update the function’s mangled name. Right now, depending on the choice
of manging algorithm, it’s possible even for top-level functions to
have their names changed, and we must account for that. The whole code is:
|
|
Finally, we call global_scope’s methods in main():
|
|
That’s it! Please note that I’ve mentioned or hinted at minor changes to the codebase. Detailing every single change this late into the project is needlessly time consuming and verbose; Gitea reports that I’ve made 677 insertions into and 215 deletions from the code. As always, I provide the source code for the compiler, and you can also take a look at the Gitea-generated diff at the time of writing. If you want to follow along, feel free to check them out!
Running Our Programs
It’s important to test all the language features that we just added. This
includes recursive definitions, nested function dependency cycles, and
uses of lambda functions. Some of the following examples will be rather
silly, but they should do a good job of checking that everything works
as we expect. Let’s start with a simple use of a recursive definition
inside a let/in. A classic definition in that form is of fix
(the fixpoint combinator):
fix f = let x = f x in x
This defines x to be f x, which by substitution becomes f (f x), and then
f (f (f x)) and so on. The fixpoint combinator allows one to write a
recursive function that doesn’t use its own name in the body. Rather,
we write a function expecting to receive ‘itself’ as a value:
fix :: (a -> a) -> a
factRec :: (Int -> Int) -> Int -> Int
factRec f x = if x == 0 then 1 else x * f x
fact :: Int -> Int
fact = fix factRec
Notice that factRec doesn’t reference itself, but rather takes
as argument a function it expects to be ‘factorial’ called f,
and uses that in its recursive case. We can write something similar
in our language, perhaps to create an infinite list of ones:
|
|
We want sumTwo to take the first two elements from the list,
and return their sum. For an infinite list of ones, we expect
this sum to be equal to 2, and it is:
Result: 2
Next, let’s try to define a function which has a mutually recursive pair
of definitions inside of a let/in. Let’s also make these expressions
reference a function from the global scope, so that we know our
dependency tracking works as expected:
|
|
Here, we have a function mergeUntil which, given two lists
and a predicate, combines the two lists as long as
the predicate returns True. It does so using a convoluted
pair of mutually recursive functions, one of which
unpacks the left list, and the other the right. Each of the
functions calls the global function if. We also use two
definitions inside of main to create the two lists we’re
going to merge. The compiler outputs the following (correct)
types:
const: forall bb bc . bc -> bb -> bc
if: Bool* -> List* Int* -> List* Int* -> List* Int*
main: Int*
mergeUntil: List* Int* -> List* Int* -> (Int* -> Bool*) -> List* Int*
sum: List* Int* -> Int*
And the result is 21, as would be expected from the sum of the numbers 1-6:
Result: 21
Let’s try lambda functions now. We can try use them for a higher-order function
like map:
|
|
In this example, we first double every element in the list, then square it, and finally take the sum. This should give us 4+16+36 = 56, and so it does:
Result: 56
Finally, let’s do some magic with a locally-declared data type. We’ll make a
“packer” that creates a wrapped instance of a type, Packed a. Since the
constructor of this data type is not globally visible, it’s not possible
to get the value back out, except by using an ‘unpacking’ function that
we provide:
|
|
Here, the packer definition returns a pair of the ‘packing’
and ‘unpacking’ functions. The ‘packing’ function simply applies
the consntructor of Packed to its argument, while the ‘unpacking’
function performs pattern matching (which is possible since the
data type is still in scope there). We expect unpack (pack 3) to
return 3, and it does:
Result: 3
Trying to pattern match, though, doesn’t work, just like we would want!
This is enough to convince me that our changes do, indeed, work! Of the ‘major’ components that I wanted to cover, only Input/Output remains! Additionally, a lobste.rs user suggested that we also cover namespacing, and perhaps we will look into that as well. Before either of those things, though, I think that I want to go through the compiler and perform another round of improvements, similarly to part 4. It’s hard to do a lot of refactoring while covering new content, since major changes need to be explained and presented for the post to make sense. I do this in part 13 - cleanup. I hope to see you there!