In the previous post, I showed that the Control Flow graphs we built of our programs match how they are really executed. This means that we can rely on these graphs to compute program information. In this post, we finally get to compute that information. Here’s a quick bit paraphrasing from last time that provides a summary of our approach:
- We will construct a finite-height lattice. Every single element of this lattice will contain information about each variable at each node in the Control Flow Graph.
- We will then define a monotonic function that update this information using the structure encoded in the CFG’s edges and nodes.
- Then, using the fixed-point algorithm, we will find the least element of the lattice, which will give us a precise description of all program variables at all points in the program.
- Because we have just validated our CFGs to be faithful to the language’s semantics, we’ll be able to prove that our algorithm produces accurate results.
Let’s jump right into it!
Choosing a Lattice
A lot of this time, we have been talking about lattices, particularly lattices of finite height. These structures represent things we know about the program, and provide operators like and that help us combine such knowledge.
The forward analysis code I present here will work with any finite-height lattice, with the additional constraint that equivalence of lattices is decidable, which comes from the implementation of the fixed-point algorithm, in which we routinely check if a function’s output is the same as its input.
The finite-height lattice L is intended to describe the state of a single
variable.
One example of a lattice that can be used as L is our
sign lattice. We’ve been using the sign lattice in our examples from the very beginning,
and we will stick with it for the purposes of this explanation. However, this
lattice alone does not describe our program, since it only talks about a single
sign; programs have lots of variables, all of which can have different signs!
So, we might go one step further and define a map lattice from variables to
their signs:
We have seen that we can turn any lattice into a map lattice , for any type of keys . In this case, we will define , and . The sign lattice has a finite height, and I’ve proven that, as long as we pick a finite set of keys, map lattices have a finite height if has a finite height. Since a program’s text is finite, is a finite set, and we have ourselves a finite-height lattice .
We’re on the right track, but even the lattice we have so far is not sufficient.
That’s because variables have different signs at different points in the program!
You might initialize a variable with x = 1, making it positive, and then
go on to compute some arbitrary function using loops and conditionals. For
each variable, we need to keep track of its sign at various points in the code.
When we defined Control Flow Graphs, we
split our programs into sequences of statements that are guaranteed to execute
together — basic blocks. For our analysis, we’ll keep per-variable for
each basic block in the program. Since basic blocks are nodes in the Control Flow
Graph of our program, our whole lattice will be as follows:
We follow the same logic we just did for the variable-sign lattice; since is a lattice of finite height, and since is a finite set, the whole map will be a lattice with a finite height.
Notice that both the sets of and depend on the program in question. The lattice we use is slightly different for each input program! We can use Agda’s parameterized modules to automaitcally parameterize all our functions over programs:
Now, let’s make the informal descriptions above into code, by instantiating
our map lattice modules. First, I invoked the code for the smaller variable-sign
lattice. This ended up being quite long, so that I could rename variables I
brought into scope. I will collapse the relevant code block; suffice to say
that I used the suffix v (e.g., renaming _⊔_ to _⊔ᵛ_) for properties
and operators to do with variable-sign maps (in Agda: VariableValuesFiniteMap).
(Click here to expand the module uses for variable-sign maps)
|
|
I then used this lattice as an argument to the map module again, to
construct the top-level lattice (in Agda: StateVariablesFiniteMap).
This also required a fair bit of code, most of it to do with renaming.
(Click here to expand the module uses for the top-level lattice)
|
|
Constructing a Monotone Function
We now have a lattice in hand; the next step is to define a function over this lattice. For us to be able to use the fixed-point algorithm on this function, it will need to be monotonic.
Our goal with static analysis is to compute information about our program; that’s what we want the function to do. When the lattice we’re using is the sign lattice, we’re trying to determine the signs of each of the variables in various parts of the program. How do we go about this?
Each piece of code in the program might change a variable’s sign. For instance,
if x has sign , and we run the statement x = x - 1, the sign of
x will be . If we have an expression y + z, we can use the signs of
y and z to compute the sign of the whole thing. This is a form
of abstract interpretation,
in which we almost-run the program, but forget some details (e.g., the
exact values of x, y, and z, leaving only their signs). The exact details
of how this partial evaluation is done are analysis-specific; in general, we
simply require an analysis to provide an evaluator. We will define
an evaluator for the sign lattice below.
From this, we know how each statement and basic block will change variables
in the function. But we have described them process as “if a variable has
sign X, it becomes sign Y” – how do we know what sign a variable has before
the code runs? Fortunately, the Control Flow Graph tells us exactly
what code could be executed before any given basic block. Recall that edges
in the graph describe all possible jumps that could occur; thus, for any
node, the incoming edges describe all possible blocks that can precede it.
This is why we spent all that time defining the predecessors function.
We proceed as follows: for any given node, find its predecessors. By accessing
our map for each predecessor, we can determine our current
best guess of variable signs at that point, in the form of a
map (more generally, map in an arbitrary analysis).
We know that any of these predecessors could’ve been the previous point of
execution; if a variable x has sign in one predecessor and
in another, it can be either one or the other when we start executing the
current block. Early on, we saw that the operator models disjunction
(“A or B”). So, we apply
to the variable-sign maps of all predecessors. The
reference Static Program Analysis text
calls this operation :
The Agda implementation uses a foldr:
|
|
Computing the “combined incoming states” for any node is a monotonic function.
This follows from the monotonicity of — in both arguments —
and the definition of foldr.
(Click here to expand the general proof)
|
|
From this, we can formally state that is monotonic. Note that the input and output lattices are different: the input lattice is the lattice of variable states at each block, and the output lattice is a single variable-sign map, representing the combined preceding state at a given node.
|
|
Above, the m₁≼m₂⇒m₁[ks]≼m₂[ks] lemma states that for two maps with the same
keys, where one map is less than another, all the values for any subset of keys
ks are pairwise less than each other (i.e. m₁[k]≼m₂[k], and m₁[l]≼m₂[l], etc.).
This follows from the definition of “less than” for maps.
So those are the two pieces: first, join all the preceding states, then use the abstract interpretation function. I opted to do both of these in bulk:
- Take an initial map, and update every basic block’s entry to be the join of its predecessors.
- In the new joined map, each key now contains the variable state at
the beginning of the block; so, apply the abstract interpretation function
via
evalto each key, computing the state at the end of the block.
I chose to do these in bulk because this way, after each application of the function, we have updated each block with exactly one round of information. The alternative — which is specified in the reference text — is to update one key at a time. The difference there is that updates to later keys might be “tainted” by updates to keys that came before them. This is probably fine (and perhaps more efficient, in that it “moves faster”), but it’s harder to reason about.
Generalized Update
To implement bulk assignment, I needed to implement the source text’s Exercise 4.26:
Exercise 4.26: Recall that denotes the function that is identical to except that it maps to . Assume and are monotone functions where and are lattices and is a set, and let . (Note that the codomain of is a map lattice.)
Show that the function defined by is monotone.
In fact, I generalized this statement to update several keys at once, as follows:
I called this operation “generalized update”.
At first, the exercise may not obviously correspond to the bulk operation I’ve described. Particularly confusing is the fact that it has two lattices, and . In fact, the exercise results in a very general theorem; we can exploit a more concrete version of the theorem by setting , resulting in an overall signature for and :
In other words, if we give the entire operation in Exercise 4.26 a type, it would look like this:
That’s still more general than we need it. This here allows us to modify any map-to-map function by updating a certain key in that function. If we just want to update keys (as we do for the purposes of static analysis), we can recover a simpler version by setting , which results in an updater , and a signature for the exercise:
This looks just like Haskell’s Data.Map.adjust function, except that it
can take the entire map into consideration when updating a key.
My generalized version takes in a list of keys to update, and makes the updater
accept a key so that its behavior can be specialized for each entry it changes.
The sketch of the implementation is in the _updating_via_ function from
the Map module, and its helper transform. Here, I collapse its definition,
since it’s not particularly important.
(Click here to see the definition of transform)
The proof of monotonicity — which is the solution to the exercise — is actually quite complicated. I will omit its description, and show it here in another collapsed block.
(Click here to see the proof of monotonicity of )
|
|
Given a proof of the exercise, all that’s left is to instantiate the theorem with the argument I described. Specifically:
In the equation for , I explicitly insert the map instead of leaving
it implicit as the textbook does. In Agda, this instantiation for joining
all predecessor looks like this (using states as the list of keys to update,
indicating that we should update every key):
|
|
And the one for evaluating all programs looks like this:
|
|
Actually, we haven’t yet seen that updateVariablesFromStmt. This is
a function that we can define using the user-provided abtract interpretation
eval. Specifically, it handles the job of updating the sign of a variable
once it has been assigned to (or doing nothing if the statement is a no-op).
|
|
The updateVariablesFromExpression is now new, and it is yet another map update,
which changes the sign of a variable k to be the one we get from running
eval on it. Map updates are instances of the generalized update; this
time, the updater is eval. The exercise requires the updater to be
monotonic, which constrains the user-provided evaluation function to be
monotonic too.
|
|
We finally write the analyze function as the composition of the two bulk updates:
|
|
Instantiating with the Sign Lattice
Thus far, I’ve been talking about the sign lattice throughout, but implementing
the Agda code in terms of a general lattice L and evaluation function eval.
In order to actually run the Agda code, we do need to provide an eval function,
which implements the logic we used above, in which a zero-sign variable
minus one was determined to be negative. For binary operators specifically,
I’ve used the table provided in the textbook; here they are:
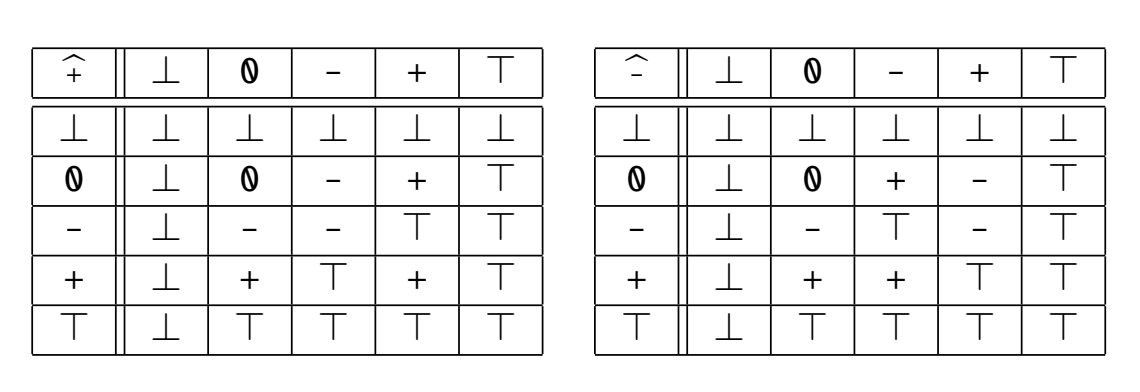
Cayley tables for abstract interpretation of plus and minus
These are pretty much common sense:
- A positive plus a positive is still positive, so
- A positive plus any sign could be any sign still, so
- Any sign plus “impossible” is impossible, so .
- etc.
The Agda encoding for the plus function is as follows, and the one for minus is similar.
|
|
As the comment in the block says, it would be incredibly tedious to verify
the monotonicity of these tables, since you would have to consider roughly
125 cases per argument: for each (fixed) sign and two other signs
, we’d need to show that .
I therefore commit the faux pas of using postulate. Fortunately, the proof
of monotonicity is not used for the execution of the program, so we will
get away with this, barring any meddling kids.
From this, all that’s left is to show that for any expression e, the
evaluation function:
is monotonic. It’s defined straightforwardly and very much like an evaluator / interpreter, suggesting that “abstract interpretation” is the correct term here.
|
|
Thought it won’t happen, it was easier to just handle the case where there’s
an undefined variable; I give it “any sign”. Otherwise, the function simply
consults the sign tables for + or -, as well as the known signs of the
variables. For natural number literals, it assigns 0 the “zero” sign, and
any other natural number the “”.
To prove monotonicity, we need to consider two variable maps (one less than
the other), and show that the abstract interpretation respects that ordering.
This boils down to the fact that the plus and minus tables are monotonic
in both arguments (thus, if their sub-expressions are evaluated monotonically
given an environment, then so is the whole addition or subtraction), and
to the fact that for two maps m₁ ≼ m₂, the values at corresponding keys
are similarly ordered: m₁[k] ≼ m₂[k]. We saw that above.
(Click to expand the proof that the evaluation function for signs is monotonic)
|
|
That’s all we need. With this, I just instantiate the Forward module we have
been working with, and make use of the result. I also used a show
function (which I defined) to stringify that output.
|
|
But wait, result? We haven’t seen a result just yet. That’s the last piece,
and it involves finally making use of the fixed-point algorithm.
Invoking the Fixed Point Algorithm
Our lattice is of finite height, and the function we have defined is monotonic (by virtue of being constructed only from map updates, which are monotonic by Exercise 4.26, and from function composition, which preserves monotonicity). We can therefore apply the fixed-point-algorithm, and compute the least fixed point:
With this, analyze is the result of our forward analysis!
In a Main.agda file, I invoked this analysis on a sample program:
testCode : Stmt
testCode =
⟨ "zero" ← (# 0) ⟩ then
⟨ "pos" ← ((` "zero") Expr.+ (# 1)) ⟩ then
⟨ "neg" ← ((` "zero") Expr.- (# 1)) ⟩ then
⟨ "unknown" ← ((` "pos") Expr.+ (` "neg")) ⟩
testProgram : Program
testProgram = record
{ rootStmt = testCode
}
open WithProg testProgram using (output; analyze-correct)
main = run {0ℓ} (putStrLn output)
The result is verbose, since it shows variable signs for each statement in the program. However, the key is the last basic block, which shows the variables at the end of the program. It reads:
{"neg" ↦ -, "pos" ↦ +, "unknown" ↦ ⊤, "zero" ↦ 0, }
Verifying the Analysis
We now have a general framework for running forward analyses: you provide
an abstract interpretation function for expressions, as well as a proof
that this function is monotonic, and you get an Agda function that takes
a program and tells you the variable states at every point. If your abstract
interpretation function is for determining the signs of expressions, the
final result is an analysis that determines all possible signs for all variables,
anywhere in the code. It’s pretty easy to instantiate this framework with
another type of forward analysis — in fact, by switching the
plus function to one that uses AboveBelow ℤ, rather than AboveBelow Sign:
plus : ConstLattice → ConstLattice → ConstLattice
plus ⊥ᶜ _ = ⊥ᶜ
plus _ ⊥ᶜ = ⊥ᶜ
plus ⊤ᶜ _ = ⊤ᶜ
plus _ ⊤ᶜ = ⊤ᶜ
plus [ z₁ ]ᶜ [ z₂ ]ᶜ = [ z₁ Int.+ z₂ ]ᶜ
we can defined a constant-propagation analysis.
{"neg" ↦ -1, "pos" ↦ 1, "unknown" ↦ 0, "zero" ↦ 0, }
However, we haven’t proved our analysis correct, and we haven’t yet made use of the CFG-semantics equivalence that we proved in the previous section. I was hoping to get to it in this post, but there was just too much to cover. So, I will get to that in the next post, where we will make use of the remaining machinery to demonstrate that the output of our analyzer matches reality.