Daniel's Blog

In the previous two posts, I covered two ways of looking at programs in my little toy language:

• In part 5, I covered the formal semantics of the programming language. These are precise rules that describe how programs are executed. These serve as the source of truth for what each statement and expression does.

  Because they are the source of truth, they capture all information about how programs are executed. To determine that a program starts in one environment and ends in another (getting a judgement $\rho_1, s \Rightarrow \rho_2$), we need to actually run the program. In fact, our Agda definitions encoding the semantics actually produce proof trees, which contain every single step of the program’s execution.

• In part 6, I covered Control Flow Graphs (CFGs), which in short arranged code into a structure that represents how execution moves from one statement or expression to the next.

  Unlike the semantics, CFGs do not capture a program’s entire execution; they merely contain the possible orders in which statements can be evaluated. Instead of capturing the exact number of iterations performed by a while loop, they encode repetition as cycles in the graph. Because they are missing some information, they’re more of an approximation of a program’s behavior.

Our analyses operate on CFGs, but it is our semantics that actually determine how a program behaves. In order for our analyses to be able to produce correct results, we need to make sure that there isn’t a disconnect between the approximation and the truth. In the previous post, I stated the property I will use to establish the connection between the two perspectives:

For each possible execution of a program according to its semantics, there exists a corresponding path through the graph.

By ensuring this property, we will guarantee that our Control Flow Graphs account for anything that might happen. Thus, a correct analysis built on top of the graphs will produce results that match reality.

A CFG contains each “basic” statement in our program, by definition; when we’re executing the program, we are therefore running code in one of the CFG’s nodes. When we switch from one node to another, there ought to be an edge between the two, since edges in the CFG encode possible control flow. We keep doing this until the program terminates (if ever).

Now, I said that there “ought to be edges” in the graph that correspond to our program’s execution. Moreover, the endpoints of these edges have to line up, since we can only switch which basic block / node we’re executing by following an edge. As a result, if our CFG is correct, then for every program execution, there is a path between the CFG’s nodes that matches the statements that we were executing.

Take the following program and CFG from the previous post as an example.

x = 2;
while x {
  x = x - 1;
}
y = x;

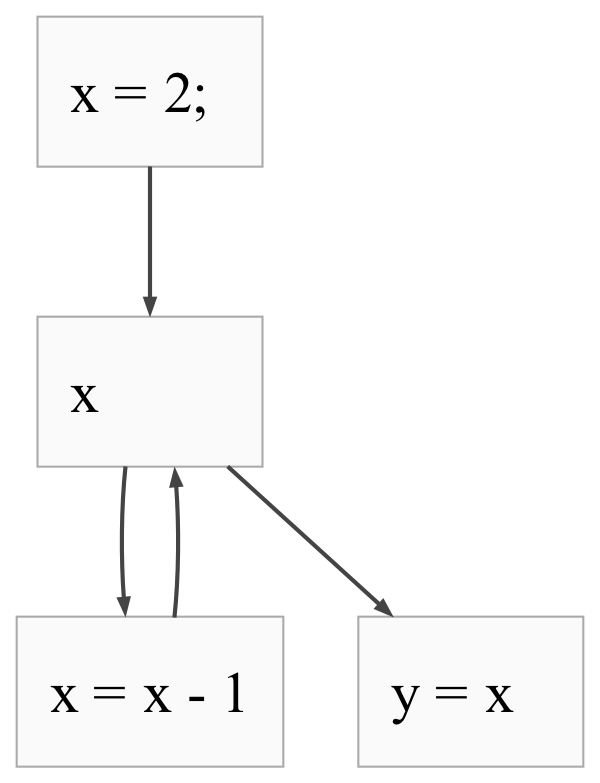
We start by executing x = 2, which is the top node in the CFG. Then, we execute the condition of the loop, x. This condition is in the second node from the top; fortunately, there exists an edge between x = 2 and x that allows for this possibility. Once we computed x, we know that it’s nonzero, and therefore we proceed to the loop body. This is the statement x = x - 1, contained in the bottom left node in the CFG. There is once again an edge between x and that node; so far, so good. Once we’re done executing the statement, we go back to the top of the loop again, following the edge back to the middle node. We then execute the condition, loop body, and condition again. At that point we have reduced x to zero, so the condition produces a falsey value. We exit the loop and execute y = x, which is allowed by the edge from the middle node to the bottom right node.

We will want to show that every possible execution of the program (e.g., with different variable assignments) corresponds to a path in the CFG. If one doesn’t, then our program can do something that our CFG doesn’t account for, which means that our analyses will not be correct.

I will define a Trace datatype, which will be an embellished path through the graph. At its core, a path is simply a list of indices together with edges that connect them. Viewed another way, it’s a list of edges, where each edge’s endpoint is the next edge’s starting point. We want to make illegal states unrepresentable, and therefore use the type system to assert that the edges are compatible. The easiest way to do this is by making our Trace indexed by its start and end points. An empty trace, containing no edges, will start and end in the same node; the :: equivalent for the trace will allow prepending one edge, starting at node i1 and ending in i2, to another trace which starts in i2 and ends in some arbitrary i3. Here’s an initial stab at that:

module _ {g : Graph} where
    open Graph g using (Index; edges; inputs; outputs)

    data Trace : Index → Index → Set where
        Trace-single : ∀ {idx : Index} → Trace idx idx
        Trace-edge : ∀ {idx₁ idx₂ idx₃ : Index} →
                     (idx₁ , idx₂) ∈ edges →
                     Trace idx₂ idx₃ → Trace idx₁ idx₃

This isn’t enough, though. Suppose you had a function that takes an evaluation judgement and produces a trace, resulting in a signature like this:

buildCfg-sufficient : ∀ {s : Stmt} {ρ₁ ρ₂ : Env} → ρ₁ , s ⇒ˢ ρ₂ →
                      let g = buildCfg s
                      in Σ (Index g × Index g) (λ (idx₁ , idx₂) → Trace {g} idx₁ idx₂)

What’s stopping this function from returning any trace through the graph, including one that doesn’t even include the statements in our program s? We need to narrow the type somewhat to require that the nodes it visits have some relation to the program execution in question.

We could do this by indexing the Trace data type by a list of statements that we expect it to match, and requiring that for each constructor, the statements of the starting node be at the front of that list. We could compute the list of executed statements in order using a recursive function on the _,_⇒ˢ_ data type. [note: I mentioned earlier that our encoding of the semantics is actually defining a proof tree, which includes every step of the computation. That's why we can write a function that takes the proof tree and extracts the executed statements. ]

That would work, but it loses a bit of information. The execution judgement contains not only each statement that was evaluated, but also the environments before and after evaluating it. Keeping those around will be useful: eventually, we’d like to state the invariant that at every CFG node, the results of our analysis match the current program environment. Thus, instead of indexing simply by the statements of code, I chose to index my Trace by the starting and ending environment, and to require it to contain evaluation judgements for each node’s code. The judgements include the statements that were evaluated, which we can match against the code in the CFG node. However, they also assert that the environments before and after are connected by that code in the language’s formal semantics. The resulting definition is as follows:

10
11
12
13
14
15
16
17
18

module _ {g : Graph} where
    open Graph g using (Index; edges; inputs; outputs)

    data Trace : Index → Index → Env → Env → Set where
        Trace-single : ∀ {ρ₁ ρ₂ : Env} {idx : Index} →
                       ρ₁ , (g [ idx ]) ⇒ᵇˢ ρ₂ → Trace idx idx ρ₁ ρ₂
        Trace-edge : ∀ {ρ₁ ρ₂ ρ₃ : Env} {idx₁ idx₂ idx₃ : Index} →
                     ρ₁ , (g [ idx₁ ]) ⇒ᵇˢ ρ₂ → (idx₁ , idx₂) ∈ edges →
                     Trace idx₂ idx₃ ρ₂ ρ₃ → Trace idx₁ idx₃ ρ₁ ρ₃

The g [ idx ] and g [ idx₁ ] represent accessing the basic block code at indices idx and idx₁ in graph g.

Our proofs of trace existence will have the same “shape” as the functions that build the graph. To prove the trace property, we’ll assume that evaluations of sub-statements correspond to traces in the sub-graphs, and use that to prove that the full statements have corresponding traces in the full graph. We built up graphs by combining sub-graphs for sub-statements, using _∙_ (overlaying two graphs), _↦_ (sequencing two graphs) and loop (creating a zero-or-more loop in the graph). Thus, to make the jump from sub-graphs to full graphs, we’ll need to prove that traces persist through overlaying, sequencing, and looping.

Take _∙_, for instance; we want to show that if a trace exists in the left operand of overlaying, it also exists in the final graph. This leads to the following statement and proof:

88
89
90
91
92
93
94
95
96
97

Trace-∙ˡ : ∀ {g₁ g₂ : Graph} {idx₁ idx₂ : Graph.Index g₁} {ρ₁ ρ₂ : Env} →
           Trace {g₁} idx₁ idx₂ ρ₁ ρ₂ →
           Trace {g₁ ∙ g₂} (idx₁ Fin.↑ˡ Graph.size g₂) (idx₂ Fin.↑ˡ Graph.size g₂) ρ₁ ρ₂
Trace-∙ˡ {g₁} {g₂} {idx₁} {idx₁} (Trace-single ρ₁⇒ρ₂)
    rewrite sym (lookup-++ˡ (Graph.nodes g₁) (Graph.nodes g₂) idx₁) =
    Trace-single ρ₁⇒ρ₂
Trace-∙ˡ {g₁} {g₂} {idx₁} (Trace-edge ρ₁⇒ρ idx₁→idx tr')
    rewrite sym (lookup-++ˡ (Graph.nodes g₁) (Graph.nodes g₂) idx₁) =
    Trace-edge ρ₁⇒ρ (ListMemProp.∈-++⁺ˡ (x∈xs⇒fx∈fxs (_↑ˡ Graph.size g₂) idx₁→idx))
                    (Trace-∙ˡ tr')

There are some details there to discuss.

• First, we have to change the indices of the returned Trace. That’s because they start out as indices into the graph g₁, but become indices into the graph g₁ ∙ g₂. To take care of this re-indexing, we have to make use of the ↑ˡ operators, which I described in this section of the previous post.

• Next, in either case, we need to show that the new index acquired via ↑ˡ returns the same basic block in the new graph as the old index returned in the original graph. Fortunately, the Agda standard library provides a proof of this, lookup-++ˡ. The resulting equality is the following:

  g₁ [ idx₁ ] ≡ (g₁ ∙ g₂) [ idx₁ ↑ˡ Graph.size g₂ ]
  

  This allows us to use the evaluation judgement in each constructor for traces in the output of the function.

• Lastly, in the Trace-edge case, we have to additionally return a proof that the edge used by the trace still exists in the output graph. This follows from the fact that we include the edges from g₁ after re-indexing them.

      ; edges = (Graph.edges g₁ ↑ˡᵉ Graph.size g₂) List.++
                (Graph.size g₁ ↑ʳᵉ Graph.edges g₂)
  

  The ↑ˡᵉ function is just a list map with ↑ˡ. Thus, if a pair of edges is in the original list (Graph.edges g₁), as is evidenced by idx₁→idx, then its re-indexing is in the mapped list. To show this, I use the utility lemma x∈xs⇒fx∈fxs. The mapped list is the left-hand-side of a List.++ operator, so I additionally use the lemma ∈-++⁺ˡ that shows membership is preserved by list concatenation.

The proof of Trace-∙ʳ, the same property but for the right-hand operand g₂, is very similar, as are the proofs for sequencing. I give their statements, but not their proofs, below.

 99
100
101

Trace-∙ʳ : ∀ {g₁ g₂ : Graph} {idx₁ idx₂ : Graph.Index g₂} {ρ₁ ρ₂ : Env} →
           Trace {g₂} idx₁ idx₂ ρ₁ ρ₂ →
           Trace {g₁ ∙ g₂} (Graph.size g₁ Fin.↑ʳ idx₁) (Graph.size g₁ Fin.↑ʳ idx₂) ρ₁ ρ₂

139
140
141

Trace-↦ˡ : ∀ {g₁ g₂ : Graph} {idx₁ idx₂ : Graph.Index g₁} {ρ₁ ρ₂ : Env} →
           Trace {g₁} idx₁ idx₂ ρ₁ ρ₂ →
           Trace {g₁ ↦ g₂} (idx₁ Fin.↑ˡ Graph.size g₂) (idx₂ Fin.↑ˡ Graph.size g₂) ρ₁ ρ₂

150
151
152

Trace-↦ʳ : ∀ {g₁ g₂ : Graph} {idx₁ idx₂ : Graph.Index g₂} {ρ₁ ρ₂ : Env} →
           Trace {g₂} idx₁ idx₂ ρ₁ ρ₂ →
           Trace {g₁ ↦ g₂} (Graph.size g₁ Fin.↑ʳ idx₁) (Graph.size g₁ Fin.↑ʳ idx₂) ρ₁ ρ₂

175
176

Trace-loop : ∀ {g : Graph} {idx₁ idx₂ : Graph.Index g} {ρ₁ ρ₂ : Env} →
             Trace {g} idx₁ idx₂ ρ₁ ρ₂ → Trace {loop g} (2 Fin.↑ʳ idx₁) (2 Fin.↑ʳ idx₂) ρ₁ ρ₂

Preserving traces is unfortunately not quite enough. The thing that we’re missing is looping: the same sub-graph can be re-traversed several times as part of execution, which suggests that we ought to be able to combine multiple traces through a loop graph into one. Using our earlier concrete example, we might have traces for evaluating x then x = x -1 with the variable x being mapped first to 2 and then to 1. These traces occur back-to-back, so we will put them together into a single trace. To prove some properties about this, I’ll define a more precise type of trace.

The key way that traces through a loop graph are combined is through the back-edges. Specifically, our loop graphs have edges from each of the output nodes to each of the input nodes. Thus, if we have two paths, both starting at the beginning of the graph and ending at the end, we know that the first path’s end has an edge to the second path’s beginning. This is enough to combine them.

This logic doesn’t work if one of the paths ends in the middle of the graph, and not on one of the outputs. That’s because there is no guarantee that there is a connecting edge.

To make things easier, I defined a new data type of “end-to-end” traces, whose first nodes are one of the graph’s inputs, and whose last nodes are one of the graph’s outputs.

27
28
29
30
31
32
33
34
35
36

    record EndToEndTrace (ρ₁ ρ₂ : Env) : Set where
        constructor MkEndToEndTrace
        field
            idx₁ : Index
            idx₁∈inputs : idx₁ ∈ inputs

            idx₂ : Index
            idx₂∈outputs : idx₂ ∈ outputs

            trace : Trace idx₁ idx₂ ρ₁ ρ₂

We can trivially lift the proofs from the previous section to end-to-end traces. For example, here’s the lifted version of the first property we proved:

110
111
112
113
114
115
116
117
118
119
120
121

EndToEndTrace-∙ˡ : ∀ {g₁ g₂ : Graph} {ρ₁ ρ₂ : Env} →
                   EndToEndTrace {g₁} ρ₁ ρ₂ →
                   EndToEndTrace {g₁ ∙ g₂} ρ₁ ρ₂
EndToEndTrace-∙ˡ {g₁} {g₂} etr = record
    { idx₁ = EndToEndTrace.idx₁ etr Fin.↑ˡ Graph.size g₂
    ; idx₁∈inputs = ListMemProp.∈-++⁺ˡ (x∈xs⇒fx∈fxs (Fin._↑ˡ Graph.size g₂)
                                                    (EndToEndTrace.idx₁∈inputs etr))
    ; idx₂ = EndToEndTrace.idx₂ etr Fin.↑ˡ Graph.size g₂
    ; idx₂∈outputs = ListMemProp.∈-++⁺ˡ (x∈xs⇒fx∈fxs (Fin._↑ˡ Graph.size g₂)
                                                    (EndToEndTrace.idx₂∈outputs etr))
    ; trace = Trace-∙ˡ (EndToEndTrace.trace etr)
    }

The other lifted properties are similar.

For looping, the proofs get far more tedious, because of just how many sources of edges there are in the output graph — they span four lines:

84
85
86
87
88
89
90
91
92
93
94

loop : Graph → Graph
loop g = record
    { size = 2 Nat.+ Graph.size g
    ; nodes = [] ∷ [] ∷ Graph.nodes g
    ; edges = (2 ↑ʳᵉ Graph.edges g) List.++
              List.map (zero ,_) (2 ↑ʳⁱ Graph.inputs g) List.++
              List.map (_, suc zero) (2 ↑ʳⁱ Graph.outputs g) List.++
              ((suc zero , zero) ∷ (zero , suc zero) ∷ [])
    ; inputs = zero ∷ []
    ; outputs = (suc zero) ∷ []
    }

I therefore made use of two helper lemmas. The first is about list membership under concatenation. Simply put, if you concatenate a bunch of lists, and one of them (l) contains some element x, then the concatenation contains x too.

82
83
84
85

concat-∈ : ∀ {a} {A : Set a} {x : A} {l : List A} {ls : List (List A)} →
           x ∈ l → l ∈ ls → x ∈ foldr _++_ [] ls
concat-∈ x∈l (here refl) = ListMemProp.∈-++⁺ˡ x∈l
concat-∈ {ls = l' ∷ ls'} x∈l (there l∈ls') = ListMemProp.∈-++⁺ʳ l' (concat-∈ x∈l l∈ls')

I then specialized this lemma for concatenated groups of edges.

162
163
164
165
166
167
168
169
170
171
172

loop-edge-groups : ∀ (g : Graph) → List (List (Graph.Edge (loop g)))
loop-edge-groups g =
    (2 ↑ʳᵉ Graph.edges g) ∷
    (List.map (zero ,_) (2 ↑ʳⁱ Graph.inputs g)) ∷
    (List.map (_, suc zero) (2 ↑ʳⁱ Graph.outputs g)) ∷
    ((suc zero , zero) ∷ (zero , suc zero) ∷ []) ∷
    []

loop-edge-help : ∀ (g : Graph) {l : List (Graph.Edge (loop g))} {e : Graph.Edge (loop g)} →
                 e ListMem.∈ l → l ListMem.∈ loop-edge-groups g →
                 e ListMem.∈ Graph.edges (loop g)

Now we can finally prove end-to-end properties of loop graphs. The simplest one is that they allow the code within them to be entirely bypassed (as when the loop body is evaluated zero times). I called this EndToEndTrace-loop⁰. The “input” node of the loop graph is index zero, while the “output” node of the loop graph is index suc zero. Thus, the key step is to show that an edge between these two indices exists:

227
228
229
230
231
232
233
234
235
236
237
238
239
240

EndToEndTrace-loop⁰ : ∀ {g : Graph} {ρ : Env} →
                      EndToEndTrace {loop g} ρ ρ
EndToEndTrace-loop⁰ {g} {ρ} =
    let
        zero→suc = loop-edge-help g (there (here refl))
                                    (there (there (there (here refl))))
    in
        record
            { idx₁ = zero
            ; idx₁∈inputs = here refl
            ; idx₂ = suc zero
            ; idx₂∈outputs = here refl
            ; trace = Trace-single [] ++⟨ zero→suc ⟩ Trace-single []
            }

The only remaining novelty is the trace field of the returned EndToEndTrace. It uses the trace concatenation operation ++⟨_⟩. This operator allows concatenating two traces, which start and end at distinct nodes, as long as there’s an edge that connects them:

21
22
23
24
25

    _++⟨_⟩_ : ∀ {idx₁ idx₂ idx₃ idx₄ : Index} {ρ₁ ρ₂ ρ₃ : Env} →
           Trace idx₁ idx₂ ρ₁ ρ₂ → (idx₂ , idx₃) ∈ edges →
           Trace idx₃ idx₄ ρ₂ ρ₃ → Trace idx₁ idx₄ ρ₁ ρ₃
    _++⟨_⟩_ (Trace-single ρ₁⇒ρ₂) idx₂→idx₃ tr = Trace-edge ρ₁⇒ρ₂ idx₂→idx₃ tr
    _++⟨_⟩_ (Trace-edge ρ₁⇒ρ₂ idx₁→idx' tr') idx₂→idx₃ tr = Trace-edge ρ₁⇒ρ₂ idx₁→idx' (tr' ++⟨ idx₂→idx₃ ⟩ tr)

The expression on line 239 of Properties.agda is simply the single-edge trace constructed from the edge 0 -> 1 that connects the start and end nodes of the loop graph. Both of those nodes is empty, so no code is evaluated in that case.

The proof for combining several traces through a loop follows a very similar pattern. However, instead of constructing a single-edge trace as we did above, it concatenates two traces from its arguments. Also, instead of using the edge from the first node to the last, it instead uses an edge from the last to the first, as I described at the very beginning of this section.

209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225

EndToEndTrace-loop² : ∀ {g : Graph} {ρ₁ ρ₂ ρ₃ : Env} →
                      EndToEndTrace {loop g} ρ₁ ρ₂ →
                      EndToEndTrace {loop g} ρ₂ ρ₃ →
                      EndToEndTrace {loop g} ρ₁ ρ₃
EndToEndTrace-loop² {g} (MkEndToEndTrace zero (here refl) (suc zero) (here refl) tr₁)
                        (MkEndToEndTrace zero (here refl) (suc zero) (here refl) tr₂) =
    let
        suc→zero = loop-edge-help g (here refl)
                                    (there (there (there (here refl))))
    in
        record
            { idx₁ = zero
            ; idx₁∈inputs = here refl
            ; idx₂ = suc zero
            ; idx₂∈outputs = here refl
            ; trace = tr₁ ++⟨ suc→zero ⟩ tr₂
            }

We now have all the pieces to show each execution of our program has a corresponding trace through a graph. Here is the whole proof:

281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296

buildCfg-sufficient : ∀ {s : Stmt} {ρ₁ ρ₂ : Env} → ρ₁ , s ⇒ˢ ρ₂ →
                      EndToEndTrace {buildCfg s} ρ₁ ρ₂
buildCfg-sufficient (⇒ˢ-⟨⟩ ρ₁ ρ₂ bs ρ₁,bs⇒ρ₂) =
    EndToEndTrace-singleton (ρ₁,bs⇒ρ₂ ∷ [])
buildCfg-sufficient (⇒ˢ-then ρ₁ ρ₂ ρ₃ s₁ s₂ ρ₁,s₁⇒ρ₂ ρ₂,s₂⇒ρ₃) =
    buildCfg-sufficient ρ₁,s₁⇒ρ₂ ++ buildCfg-sufficient ρ₂,s₂⇒ρ₃
buildCfg-sufficient (⇒ˢ-if-true ρ₁ ρ₂ _ _ s₁ s₂ _ _ ρ₁,s₁⇒ρ₂) =
    EndToEndTrace-∙ˡ (buildCfg-sufficient ρ₁,s₁⇒ρ₂)
buildCfg-sufficient (⇒ˢ-if-false ρ₁ ρ₂ _ s₁ s₂ _ ρ₁,s₂⇒ρ₂) =
    EndToEndTrace-∙ʳ {buildCfg s₁} (buildCfg-sufficient ρ₁,s₂⇒ρ₂)
buildCfg-sufficient (⇒ˢ-while-true ρ₁ ρ₂ ρ₃ _ _ s _ _ ρ₁,s⇒ρ₂ ρ₂,ws⇒ρ₃) =
    EndToEndTrace-loop² {buildCfg s}
                        (EndToEndTrace-loop {buildCfg s} (buildCfg-sufficient ρ₁,s⇒ρ₂))
                        (buildCfg-sufficient ρ₂,ws⇒ρ₃)
buildCfg-sufficient (⇒ˢ-while-false ρ _ s _) =
    EndToEndTrace-loop⁰ {buildCfg s} {ρ}

We proceed by checking what inference rule was used to execute a particular statement, [note: Precisely, we proceed by induction on the derivation of $\rho_1, s \Rightarrow \rho_2$. ] because that’s what tells us what the program did in that particular moment.

• When executing a basic statement, we know that we constructed a singleton graph that contains one node with that statement. Thus, we can trivially construct a single-step trace without any edges.

• When executing a sequence of statements, we have two induction hypotheses. These state that the sub-graphs we construct for the first and second statement have the trace property. We also have two evaluation judgements (one for each statement), which means that we can apply that property to get traces. The buildCfg function sequences the two graphs, and we can sequence the two traces through them, resulting in a trace through the final output.

• For both the then and else cases of evaluating an if statement, we observe that buildCfg overlays the sub-graphs of the two branches using _∙_. We also know that the two sub-graphs have the trace property.

  • In the then case, since we have an evaluation judgement for s₁ (in variable ρ₁,s₁⇒ρ₂), we conclude that there’s a correct trace through the then sub-graph. Since that graph is the left operand of _∙_, we use EndToEndTrace-∙ˡ to show that the trace is preserved in the full graph.
  • In the else case things are symmetric. We are evaluating s₂, with a judgement given by ρ₁,s₂⇒ρ₂. We use that to conclude that there’s a trace through the graph built from s₂. Since this sub-graph is the right operand of _∙_, we use EndToEndTrace-∙ʳ to show that it’s preserved in the full graph.

• For the true case of while, we have two evaluation judgements: one for the body and one for the loop again, this time in a new environment. They are stored in ρ₁,s⇒ρ₂ and ρ₂,ws⇒ρ₃, respectively. The statement being evaluated by ρ₂,ws⇒ρ₃ is actually the exact same statement that’s being evaluated at the top level of the proof. Thus, we can use EndToEndTrace-loop², which sequences two traces through the same graph.

  We also use EndToEndTrace-loop to lift the trace through buildCfg s into a trace through buildCfg (while e s).

• For the false case of the while, we don’t execute any instructions, and finish evaluating right away. This corresponds to the do-nothing trace, which we have established exists using EndToEndTrace-loop⁰.

That’s it! We have now validated that the Control Flow Graphs we construct match the semantics of the programming language, which makes them a good input to our static program analyses. We can finally start writing those!

We have all the pieces we need to define a formally-verified forward analysis:

• We have used the framework of lattices to encode the precision of program analysis outputs. Smaller elements in a lattice are more specific, meaning more useful information.
• We have implemented fixed-point algorithm, which finds the smallest solutions to equations in the form $f(x) = x$ for monotonic functions over lattices. By defining our analysis as such a function, we can apply the algorithm to find the most precise steady-state description of our program.
• We have defined how our programs are executed, which is crucial for defining “correctness”.

Here’s how these pieces will fit together. We will construct a finite-height lattice. Every single element of this lattice will contain information about each variable at each node in the Control Flow Graph. We will then define a monotonic function that updates this information using the structure encoded in the CFG’s edges and nodes. Then, using the fixed-point algorithm, we will find the least element of the lattice, which will give us a precise description of all program variables at all points in the program. Because we have just validated our CFGs to be faithful to the language’s semantics, we’ll be able to prove that our algorithm produces accurate results.

The next post or two will be the last stretch; I hope to see you there!