Daniel's Blog

In the previous section, I’ve given a formal definition of the programming language that I’ve been trying to analyze. This formal definition serves as the “ground truth” for how our little imperative programs are executed; however, program analyses (especially in practice) seldom take the formal semantics as input. Instead, they focus on more pragmatic program representations from the world of compilers. One such representation are Control Flow Graphs (CFGs). That’s what I want to discuss in this post.

Let’s start by building some informal intuition. CFGs are pretty much what their name suggests: they are a type of graph; their edges show how execution might jump from one piece of code to another (how control might flow).

For example, take the below program.

x = ...;
if x {
  x = 1;
} else {
  x = 0;
}
y = x;

The CFG might look like this:

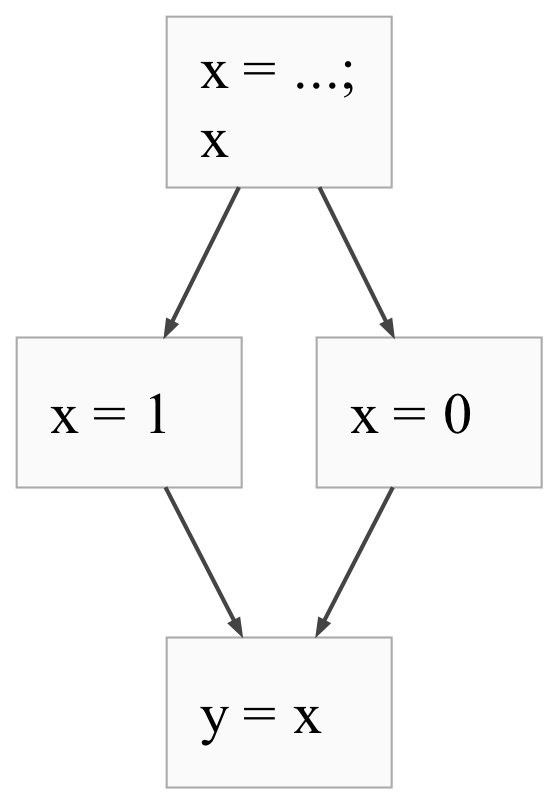
Here, the initialization of x with ..., as well as the if condition (just x), are guaranteed to execute one after another, so they occupy a single node. From there, depending on the condition, the control flow can jump to one of the branches of the if statement: the “then” branch if the condition is truthy, and the “else” branch if the condition is falsy. As a result, there are two arrows coming out of the initial node. Once either branch is executed, control always jumps to the code right after the if statement (the y = x). Thus, both the x = 1 and x = 0 nodes have a single arrow to the y = x node.

As another example, if you had a loop:

x = ...;
while x {
  x = x - 1;
}
y = x;

The CFG would look like this:

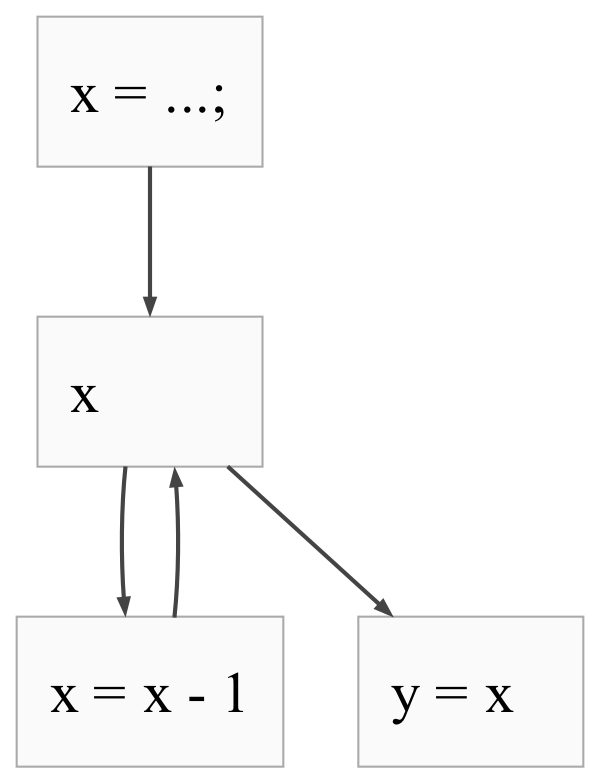
Here, the condition of the loop (x) is not always guaranteed to execute together with the code that initializes x. That’s because the condition of the loop is checked after every iteration, whereas the code before the loop is executed only once. As a result, x = ... and x occupy distinct CFG nodes. From there, the control flow can proceed in two different ways, depending on the value of x. If x is truthy, the program will proceed to the loop body (decrementing x). If x is falsy, the program will skip the loop body altogether, and go to the code right after the loop (y = x). This is indicated by the two arrows going out of the x node. After executing the body, we return to the condition of the loop to see if we need to run another iteration. Because of this, the decrementing node has an arrow back to the loop condition.

Now, let’s be a bit more precise. Control Flow Graphs are defined as follows:

• The nodes are basic blocks. Paraphrasing Wikipedia’s definition, a basic block is a piece of code that has only one entry point and one exit point.

  The one-entry-point rule means that it’s not possible to jump into the middle of the basic block, executing only half of its instructions. The execution of a basic block always begins at the top. Symmetrically, the one-exit-point rule means that you can’t jump away to other code, skipping some instructions. The execution of a basic block always ends at the bottom.

  As a result of these constraints, when running a basic block, you are guaranteed to execute every instruction in exactly the order they occur in, and execute each instruction exactly once.

• The edges are jumps between basic blocks. We’ve already seen how if and while statements introduce these jumps.

Basic blocks can only be made of code that doesn’t jump (otherwise, we violate the single-exit-point policy). In the previous post, we defined exactly this kind of code as simple statements. So, in our control flow graph, nodes will be sequences of simple statements.

At an abstract level, it’s easy to say “it’s just a graph where X is Y” about anything. It’s much harder to give a precise definition of such a graph, particularly if you want to rule out invalid graphs (e.g., ones with edges pointing nowhere). In Agda, I chose the represent a CFG with two lists: one of nodes, and one of edges. Each node is simply a list of BasicStmts, as I described in a preceding paragraph. An edge is simply a pair of numbers, each number encoding the index of the node connected by the edge.

Here’s where it gets a little complicated. I don’t want to use plain natural numbers for indices, because that means you can easily introduce “broken” edge. For example, what if you have 4 nodes, and you have an edge (5, 5)? To avoid this, I picked the finite natural numbers represented by Fin as endpoints for edges.

data Fin : ℕ → Set where
  zero : Fin (suc n)
  suc  : (i : Fin n) → Fin (suc n)

Specifically, Fin n is the type of natural numbers less than n. Following this definition, Fin 3 represents the numbers 0, 1 and 2. These are represented using the same constructors as Nat: zero and suc. The type of zero is Fin (suc n) for any n; this makes sense because zero is less than any number plus one. For suc, the bound n of the input i is incremented by one, leading to another suc n in the final type. This makes sense because if i < n, then i + 1 < n + 1. I’ve previously explained this data type in another post on this site.

Here’s my definition of Graphs written using Fin:

24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

    constructor MkGraph
    field
        size : ℕ

    Index : Set
    Index = Fin size

    Edge : Set
    Edge = Index × Index

    field
        nodes : Vec (List BasicStmt) size
        edges : List Edge
        inputs : List Index
        outputs : List Index

I explicitly used a size field, which determines how many nodes are in the graph, and serves as the upper bound for the edge indices. From there, an index Index into the node list is just a natural number less than size, [note: Ther are size natural numbers less than size:
0, 1, ..., size - 1. ] and an edge is just a pair of indices. The graph then contains a vector (exact-length list) nodes of all the basic blocks, and then a list of edges edges.

There are two fields here that I have not yet said anything about: inputs and outputs. When we have a complete CFG for our programs, these fields are totally unnecessary. However, as we are building the CFG, these will come in handy, by telling us how to stitch together smaller sub-graphs that we’ve already built. Let’s talk about that next.

Suppose you’re building a CFG for a program in the following form:

code1;
code2;

Where code1 and code2 are arbitrary pieces of code, which could include statements, loops, and pretty much anything else. Besides the fact that they occur one after another, these pieces of code are unrelated, and we can build CFGs for each one them independently. However, the fact that code1 and code2 are in sequence means that the full control flow graph for the above program should have edges going from the nodes in code1 to the nodes in code2. Of course, not every node in code1 should have such edges: that would mean that after executing any “basic” sequence of instructions, you could suddenly decide to skip the rest of code1 and move on to executing code2.

Thus, we need to be more precise about what edges we need to insert; we want to insert edges between the “final” nodes in code1 (where control ends up after code1 is finished executing) and the “initial” nodes in code2 (where control would begin once we started executing code2). Those are the outputs and inputs, respectively. When stitching together sequenced control graphs, we will connect each of the outputs of one to each of the inputs of the other.

This is defined by the operation g₁ ↦ g₂, which sequences two graphs g₁ and g₂:

72
73
74
75
76
77
78
79
80
81
82

_↦_ : Graph → Graph → Graph
_↦_ g₁ g₂ = record
    { size = Graph.size g₁ Nat.+ Graph.size g₂
    ; nodes = Graph.nodes g₁ ++ Graph.nodes g₂
    ; edges = (Graph.edges g₁ ↑ˡᵉ Graph.size g₂) List.++
              (Graph.size g₁ ↑ʳᵉ Graph.edges g₂) List.++
              (List.cartesianProduct (Graph.outputs g₁ ↑ˡⁱ Graph.size g₂)
                                     (Graph.size g₁ ↑ʳⁱ Graph.inputs g₂))
    ; inputs = Graph.inputs g₁ ↑ˡⁱ Graph.size g₂
    ; outputs = Graph.size g₁ ↑ʳⁱ Graph.outputs g₂
    }

The definition starts out pretty innocuous, but gets a bit complicated by the end. The sum of the numbers of nodes in the two operands becomes the new graph size, and the nodes from the two graphs are all included in the result. Then, the definitions start making use of various operators like ↑ˡᵉ and ↑ʳᵉ; these deserve an explanation.

The tricky thing is that when we’re concatenating lists of nodes, we are changing some of the indices of the elements within. For instance, in the lists [x] and [y], the indices of both x and y are 0; however, in the concatenated list [x, y], the index of x is still 0, but the index of y is 1. More generally, when we concatenate two lists l1 and l2, the indices into l1 remain unchanged, whereas the indices l2 are shifted by length l1.

Actually, that’s not all there is to it. The values of the indices into the left list don’t change, but their types do! They start as Fin (length l1), but for the whole list, these same indices will have type Fin (length l1 + length l2)).

To help deal with this, Agda provides the operators ↑ˡ and ↑ʳ that implement this re-indexing and re-typing. The former implements “re-indexing on the left” – given an index into the left list l1, it changes its type by adding the other list’s length to it, but keeps the index value itself unchanged. The latter implements “re-indexing on the right” – given an index into the right list l2, it adds the length of the first list to it (shifting it), and does the same to its type.

The definition leads to the following equations:

l1 : Vec A n
l2 : Vec A m

idx1 : Fin n -- index into l1
idx2 : Fin m -- index into l2

l1 [ idx1 ] ≡ (l1 ++ l2) [ idx1 ↑ˡ m ]
l2 [ idx2 ] ≡ (l1 ++ l2) [ n ↑ʳ idx2 ]

The operators used in the definition above are just versions of the same re-indexing operators. The ↑ˡᵉ operator applies ↑ˡ to all the (e)dges in a graph, and the ↑ˡⁱ applies it to all the (i)ndices in a list (like inputs and outputs).

Given these definitions, hopefully the intent with the rest of the definition is not too hard to see. The edges in the new graph come from three places: the graph g₁ and g₂, and from creating a new edge from each of the outputs of g₁ to each of the inputs of g₂. We keep the inputs of g₁ as the inputs of the whole graph (since g₁ comes first), and symmetrically we keep the outputs of g₂. Of course, we do have to re-index them to keep them pointing at the right nodes.

Another operation we will need is “overlaying” two graphs: this will be like placing them in parallel, without adding jumps between the two. We use this operation when combining the sub-CFGs of the “if” and “else” branches of an if/else, which both follow the condition, and both proceed to the code after the conditional.

59
60
61
62
63
64
65
66
67
68
69

_∙_ : Graph → Graph → Graph
_∙_ g₁ g₂ = record
    { size = Graph.size g₁ Nat.+ Graph.size g₂
    ; nodes = Graph.nodes g₁ ++ Graph.nodes g₂
    ; edges = (Graph.edges g₁ ↑ˡᵉ Graph.size g₂) List.++
              (Graph.size g₁ ↑ʳᵉ Graph.edges g₂)
    ; inputs = (Graph.inputs g₁ ↑ˡⁱ Graph.size g₂) List.++
               (Graph.size g₁ ↑ʳⁱ Graph.inputs g₂)
    ; outputs = (Graph.outputs g₁ ↑ˡⁱ Graph.size g₂) List.++
                (Graph.size g₁ ↑ʳⁱ Graph.outputs g₂)
    }

Everything here is just concatenation; we pool together the nodes, edges, inputs, and outputs, and the main source of complexity is the re-indexing.

The one last operation, which we will use for while loops, is looping. This operation simply connects the outputs of a graph back to its inputs (allowing looping), and also allows the body to be skipped. This is slightly different from the graph for while loops I showed above; the reason for that is that I currently don’t include the conditional expressions in my CFG. This is a limitation that I will address in future work.

85
86
87
88
89
90
91
92
93
94

loop g = record
    { size = 2 Nat.+ Graph.size g
    ; nodes = [] ∷ [] ∷ Graph.nodes g
    ; edges = (2 ↑ʳᵉ Graph.edges g) List.++
              List.map (zero ,_) (2 ↑ʳⁱ Graph.inputs g) List.++
              List.map (_, suc zero) (2 ↑ʳⁱ Graph.outputs g) List.++
              ((suc zero , zero) ∷ (zero , suc zero) ∷ [])
    ; inputs = zero ∷ []
    ; outputs = (suc zero) ∷ []
    }

Given these thee operations, I construct Control Flow Graphs as follows, where singleton creates a new CFG node with the given list of simple statements:

122
123
124
125

buildCfg ⟨ bs₁ ⟩ = singleton (bs₁ ∷ [])
buildCfg (s₁ then s₂) = buildCfg s₁ ↦ buildCfg s₂
buildCfg (if _ then s₁ else s₂) = buildCfg s₁ ∙ buildCfg s₂
buildCfg (while _ repeat s) = loop (buildCfg s)

Throughout this, I’ve been liberal to include empty CFG nodes as was convenient. This is a departure from the formal definition I gave above, but it makes things much simpler.

To integrate Control Flow Graphs into our lattice-based program analyses, we’ll need to do a couple of things. First, upon reading the reference Static Program Analysis text, one sees a lot of quantification over the predecessors or successors of a given CFG node. For example, the following equation is from Chapter 5:

To compute the $\textit{JOIN}$ function (which we have not covered yet) for a given CFG node, we need to iterate over all of its predecessors, and combine their static information using $\sqcup$, which I first explained several posts ago. To be able to iterate over them, we need to be able to retrieve the predecessors of a node from a graph!

Our encoding does not make computing the predecessors particularly easy; to check if two nodes are connected, we need to check if an Index-Index pair corresponding to the nodes is present in the edges list. To this end, we need to be able to compare edges for equality. Fortunately, it’s relatively straightforward to show that our edges can be compared in such a way; after all, they are just pairs of Fins, and Fins and products support these comparisons.

149
150
151
152

module _ (g : Graph) where
    open import Data.Product.Properties as ProdProp using ()
    private _≟_ = ProdProp.≡-dec (FinProp._≟_ {Graph.size g})
                                 (FinProp._≟_ {Graph.size g})

Next, if we can compare edges for equality, we can check if an edge is in a list. Agda provides a built-in function for this:

154

    open import Data.List.Membership.DecPropositional (_≟_) using (_∈?_)

To find the predecessors of a particular node, we go through all other nodes in the graph and see if there’s an edge there between those nodes and the current one. This is preferable to simply iterating over the edges because we may have duplicates in that list (why not?).

165
166

    predecessors : (Graph.Index g) → List (Graph.Index g)
    predecessors idx = List.filter (λ idx' → (idx' , idx) ∈? (Graph.edges g)) indices

Above, indices is a list of all the node identifiers in the graph. Since the graph has size nodes, the indices of all these nodes are simply the values 0, 1, …, size - 1. I defined a special function finValues to compute this list, together with a proof that this list is unique.

127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143

private
    z≢sf : ∀ {n : ℕ} (f : Fin n) → ¬ (zero ≡ suc f)
    z≢sf f ()

    z≢mapsfs : ∀ {n : ℕ} (fs : List (Fin n)) → All (λ sf → ¬ zero ≡ sf) (List.map suc fs)
    z≢mapsfs [] = []
    z≢mapsfs (f ∷ fs') = z≢sf f ∷ z≢mapsfs fs'

    finValues : ∀ (n : ℕ) → Σ (List (Fin n)) Unique
    finValues 0 = ([] , Utils.empty)
    finValues (suc n') =
        let
            (inds' , unids') = finValues n'
        in
            ( zero ∷ List.map suc inds'
            , push (z≢mapsfs inds') (Unique-map suc suc-injective unids')
            )

Another important property of finValues is that each node identifier is present in the list, so that our computation written by traversing the node list do not “miss” nodes.

145
146
147

    finValues-complete : ∀ (n : ℕ) (f : Fin n) → f ListMem.∈ (proj₁ (finValues n))
    finValues-complete (suc n') zero = RelAny.here refl
    finValues-complete (suc n') (suc f') = RelAny.there (x∈xs⇒fx∈fxs suc (finValues-complete n' f'))

We can specialize these definitions for a particular graph g:

156
157
158
159
160
161
162
163

    indices : List (Graph.Index g)
    indices = proj₁ (finValues (Graph.size g))

    indices-complete : ∀ (idx : (Graph.Index g)) → idx ListMem.∈ indices
    indices-complete = finValues-complete (Graph.size g)

    indices-Unique : Unique indices
    indices-Unique = proj₂ (finValues (Graph.size g))

To recap, we now have:

• A way to build control flow graphs from programs
• A list (unique’d and complete) of all nodes in the control flow graph so that we can iterate over them when the algorithm demands.
• A ‘predecessors’ function, which will be used by our static program analyses, implemented as an iteration over the list of nodes.

All that’s left is to connect our predecessors function to edges in the graph. The following definitions say that when an edge is in the graph, the starting node is listed as a predecessor of the ending node, and vise versa.

168
169
170
171
172
173
174
175
176
177

    edge⇒predecessor : ∀ {idx₁ idx₂ : Graph.Index g} → (idx₁ , idx₂) ListMem.∈ (Graph.edges g) →
                    idx₁ ListMem.∈ (predecessors idx₂)
    edge⇒predecessor {idx₁} {idx₂} idx₁,idx₂∈es =
        ∈-filter⁺ (λ idx' → (idx' , idx₂) ∈? (Graph.edges g))
                  (indices-complete idx₁) idx₁,idx₂∈es

    predecessor⇒edge : ∀ {idx₁ idx₂ : Graph.Index g} → idx₁ ListMem.∈ (predecessors idx₂) →
                       (idx₁ , idx₂) ListMem.∈ (Graph.edges g)
    predecessor⇒edge {idx₁} {idx₂} idx₁∈pred =
        proj₂ (∈-filter⁻ (λ idx' → (idx' , idx₂) ∈? (Graph.edges g)) {v = idx₁} {xs = indices} idx₁∈pred )

I’ve described Control Flow Graphs as a compiler-centric representation of the program. Unlike the formal semantics from the previous post, CFGs do not reason about the dynamic behavior of the code. Instead, they capture the possible paths that execution can take through the instructions. In that sense, they are more of an approximation of what the program will do. This is good: because of Rice’s theorem, we can’t do anything other than approximating without running the program.

However, an incorrect approximation is of no use at all. Since the CFGs we build will be the core data type used by our program analyses, it’s important that they are an accurate, if incomplete, representation. Specifically, because most of our analyses reason about possible outcomes — we report what sign each variable could have, for instance — it’s important that we don’t accidentally omit cases that can happen in practice from our CFGs. Formally, this means that for each possible execution of a program according to its semantics, there exists a corresponding path through the graph. [note: The converse is desirable too: that the graph has only paths that correspond to possible executions of the program. One graph that violates this property is the strongly-connected graph of all basic blocks in a program. Analyzing such a graph would give us an overly-conservative estimation; since anything can happen, most of our answers will likely be too general to be of any use. If, on the other hand, only the necessary graph connections exist, we can be more precise.

However, proving this converse property (or even stating it precisely) is much harder, because our graphs are somewhat conservative already. There exist programs in which the condition of an if-statement is always evaluated to false, but our graphs always have edges for both the "then" and "else" cases. Determining whether a condition is always false (e.g.) is undecidable thanks to Rice's theorem (again), so we can't rule it out. Instead, we could broaden "all possible executions" to "all possible executions where branching conditions can produce arbitrary results", but this is something else entirely.

For the time being, I will leave this converse property aside. As a result, our approximations might be "too careful". However, they will at the very least be sound. ]

In the next post, I will prove that this property holds for the graphs shown here and the formal semantics I defined earlier. I hope to see you there!